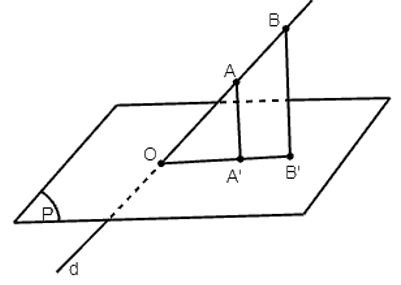
Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d và khác O; các điểm A’, B’ thuộc (P)

Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d và khác O; các điểm A’, B’ thuộc (P) thỏa mãn AA’ ⊥ (P), BB’ ⊥ (P). Chứng minh rằng $\frac{A{A}^{\text{'}}}{B{B}^{\text{'}}}=\frac{OA}{OB}.$

Trả lời