Câu hỏi:
30/01/2024 60
Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho AB = CD. Khẳng định nào sau đây sai?
Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho AB = CD. Khẳng định nào sau đây sai?
A. ∆AOB = ∆COD;
A. ∆AOB = ∆COD;
B. ;
B. ;
Đáp án chính xác
C. ;
D. .
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
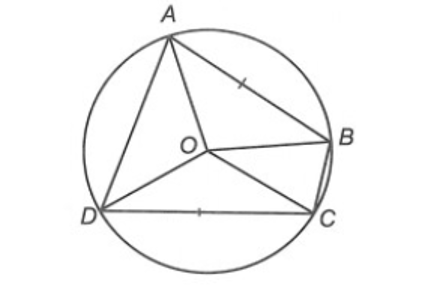
⦁ Xét ∆AOB và ∆COD, có:
OA = OC (= R)
OB = OD (= R)
AB = CD (giả thiết)
Do đó ∆AOB = ∆COD (c.c.c)
Vì vậy phương án A đúng.
⦁ Ta có ∆AOB = ∆COD (chứng minh trên)
Suy ra và (các cặp góc tương ứng)
Vì vậy phương án B sai, phương án C, D đúng.
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC = ∆IHK, biết AB = 5 cm, HK = 9 cm và IK = 12 cm. Chu vi ∆ABC bằng:
Cho ∆ABC = ∆IHK, biết AB = 5 cm, HK = 9 cm và IK = 12 cm. Chu vi ∆ABC bằng:
Xem đáp án »
30/01/2024
67
Câu 2:
Cho là góc nhọn. Trên tia Ox và Oy, lần lượt lấy hai điểm A và B sao cho OA = OB. Gọi M là trung điểm của đoạn thẳng AB. Kết luận nào sau đây đúng nhất?
Cho là góc nhọn. Trên tia Ox và Oy, lần lượt lấy hai điểm A và B sao cho OA = OB. Gọi M là trung điểm của đoạn thẳng AB. Kết luận nào sau đây đúng nhất?
Xem đáp án »
30/01/2024
60


