Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit y = logax, y = logbx
12
23/10/2024
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit y = logax, y = logbx, y = logcx được cho bởi Hình 4. Kết luận nào sau đây là đúng đối với ba số a, b, c?
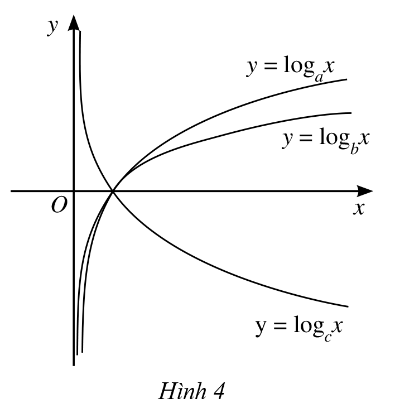
A. c > b > a;
B. a > b > c;
C. b > a > c;
D. c > a > b.
Trả lời
Đáp án đúng là: C
Hàm số lôgarit y = logc x nghịch biến trên (0; +∞) nên 0 < c < 1. (1)
Hàm số lôgarit y = logax, y = logbx đồng biến trên (0; +∞) nên a > 1 và b > 1 (2)
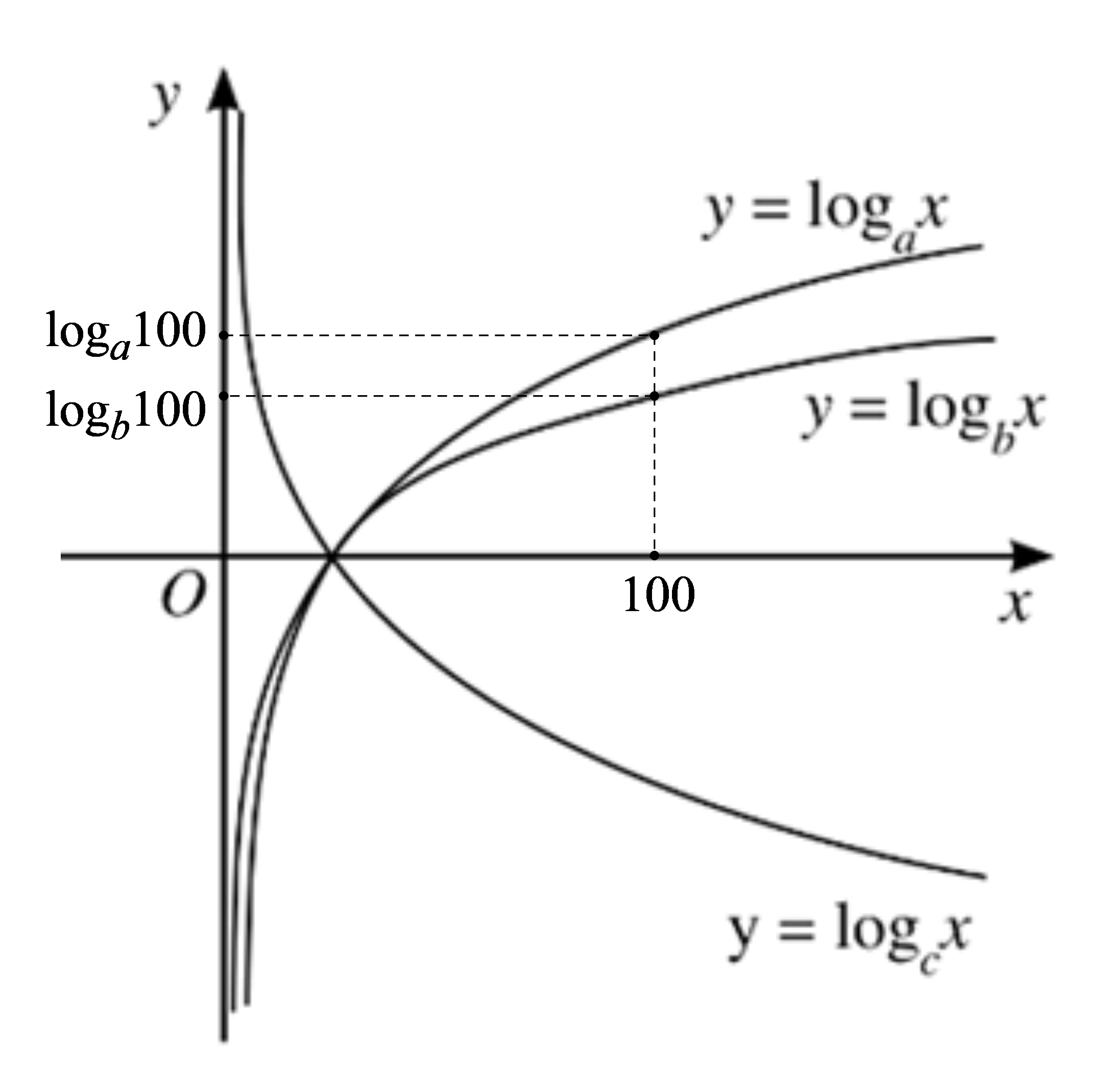
Với x = 100, từ đồ thị ta thấy:
(do 100 > 1) (3)
Từ (1), (2) và (3) ta có: b > a > c.


