Câu hỏi:
31/01/2024 66
Cho ∆ABC vuông tại A. Gọi M là trung điểm AC. Kẻ AH ⊥ BM tại H, CK ⊥ BM tại K. So sánh AB và .
Cho ∆ABC vuông tại A. Gọi M là trung điểm AC. Kẻ AH ⊥ BM tại H, CK ⊥ BM tại K. So sánh AB và .
A. ;
A. ;
B. ;
C. ;
D. Không thể so sánh được.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
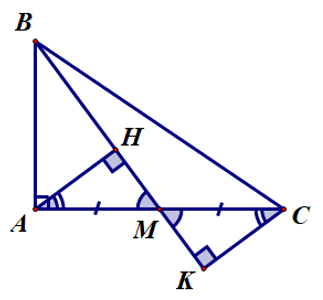
Ta có AH ⊥ BM (giả thiết) và CK ⊥ BM (giả thiết).
Suy ra AH // CK.
Do đó (cặp góc so le trong).
Xét ∆HAM và ∆KCM, có:
(hai góc đối đỉnh).
MA = MC (M là trung điểm AC).
(chứng minh trên).
Do đó ∆HAM = ∆KCM (g.c.g).
Suy ra MH = MK (cặp cạnh tương ứng).
Ta có đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC; đoạn thẳng BM là đường xiên kẻ từ điểm B đến đường thẳng AC.
Suy ra BA < BM.
Do đó BA < BH + HM (1) và BA < BK – MK (2).
Lấy (1) + (2) vế theo vế ta được 2BA < BH + HM + BK – MK.
Mà HM = MK (chứng minh trên).
Do đó 2AB < BH + BK.
Suy ra .
Vậy ta chọn đáp án B.
Đáp án đúng là: B
Ta có AH ⊥ BM (giả thiết) và CK ⊥ BM (giả thiết).
Suy ra AH // CK.
Do đó (cặp góc so le trong).
Xét ∆HAM và ∆KCM, có:
(hai góc đối đỉnh).
MA = MC (M là trung điểm AC).
(chứng minh trên).
Do đó ∆HAM = ∆KCM (g.c.g).
Suy ra MH = MK (cặp cạnh tương ứng).
Ta có đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC; đoạn thẳng BM là đường xiên kẻ từ điểm B đến đường thẳng AC.
Suy ra BA < BM.
Do đó BA < BH + HM (1) và BA < BK – MK (2).
Lấy (1) + (2) vế theo vế ta được 2BA < BH + HM + BK – MK.
Mà HM = MK (chứng minh trên).
Do đó 2AB < BH + BK.
Suy ra .
Vậy ta chọn đáp án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho ∆ABC vuông tại B. Trên đường thẳng BC lấy điểm I, J, K sao cho AI < AJ < AK. Hỏi B là hình chiếu của các điểm nào lên đường thẳng AB?
Câu 3:
Cho ∆ABC vuông tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. So sánh độ dài các cạnh EA và BF.
Cho ∆ABC vuông tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. So sánh độ dài các cạnh EA và BF.
Câu 4:
Cho ∆ABC. Vẽ AD ⊥ BC, BE ⊥ AC, CF ⊥ AB (D ∈ BC, E ∈ AC, F ∈ AB). So sánh AD + BE + CF và chu vi C của ∆ABC.
Cho ∆ABC. Vẽ AD ⊥ BC, BE ⊥ AC, CF ⊥ AB (D ∈ BC, E ∈ AC, F ∈ AB). So sánh AD + BE + CF và chu vi C của ∆ABC.
Câu 5:
Cho ∆MNP vuông tại M. Vẽ MH ⊥ NP tại H. Trên cạnh NP lấy điểm E sao cho NE = MN. Trên cạnh MP lấy điểm F sao cho MF = MH. Khoảng cách từ E đến đường thẳng MP là đoạn thẳng:
Cho ∆MNP vuông tại M. Vẽ MH ⊥ NP tại H. Trên cạnh NP lấy điểm E sao cho NE = MN. Trên cạnh MP lấy điểm F sao cho MF = MH. Khoảng cách từ E đến đường thẳng MP là đoạn thẳng:
Câu 6:
Cho ∆ABC vuông tại A. Kẻ AH ⊥ BC (H ∈ BC). Có bao nhiêu đường vuông góc kẻ từ các điểm A, B, C đến các đường thẳng có trong hình bên?
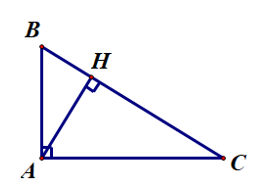
Cho ∆ABC vuông tại A. Kẻ AH ⊥ BC (H ∈ BC). Có bao nhiêu đường vuông góc kẻ từ các điểm A, B, C đến các đường thẳng có trong hình bên?
Câu 7:
Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC.
So sánh BC và tổng DH + DK.
Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC.
So sánh BC và tổng DH + DK.Câu 8:
Cho ∆ABC có , . Gọi H là chân đường vuông góc kẻ từ B. Khẳng định nào sau đây đúng?
Câu 9:
Hình bên mô tả một chiếc thang đứng hình chữ A là tam giác ABC. Do chiếc thang hơi ngắn nên một người thợ đã nối thêm 2 thanh gỗ bằng nhau BM và CN lần lượt vào hai cạnh AB, AC. Để giữ thăng bằng và cố định chiếc thang nên người thợ này muốn đóng thêm 2 thanh gỗ bằng nhau là BN và CM. Biết BC = 0,6 m, MN = 0,9 m. Em hãy cho biết độ dài thanh gỗ BN cần dài ít nhất bao nhiêu là hợp lí?
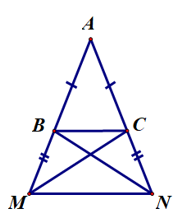
Hình bên mô tả một chiếc thang đứng hình chữ A là tam giác ABC. Do chiếc thang hơi ngắn nên một người thợ đã nối thêm 2 thanh gỗ bằng nhau BM và CN lần lượt vào hai cạnh AB, AC. Để giữ thăng bằng và cố định chiếc thang nên người thợ này muốn đóng thêm 2 thanh gỗ bằng nhau là BN và CM. Biết BC = 0,6 m, MN = 0,9 m. Em hãy cho biết độ dài thanh gỗ BN cần dài ít nhất bao nhiêu là hợp lí?
Câu 11:
Trong hình bên có bao nhiêu đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT?
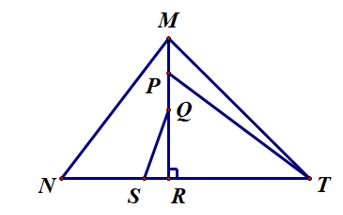
Trong hình bên có bao nhiêu đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT?
Câu 12:
Cho ∆ABC có AD là đường cao như hình bên.
Trong ba cạnh AB, AD, AC, cạnh nào ngắn nhất?
Câu 14:
Cho ∆ABC vuông tại A, biết AB = 10 cm. Trên đường thẳng AC, lấy hai điểm E và F sao cho AE = 3 cm, AF = 5 cm. So sánh CA, CB, CE và CF.
Cho ∆ABC vuông tại A, biết AB = 10 cm. Trên đường thẳng AC, lấy hai điểm E và F sao cho AE = 3 cm, AF = 5 cm. So sánh CA, CB, CE và CF.


