Câu hỏi:
31/01/2024 54
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G. Đẳng thức nào sau đây đúng?
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G. Đẳng thức nào sau đây đúng?
A. ;
B. ;
C. AD + BE + CF < AB + BC + AC;
D. Đáp án A, C đúng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
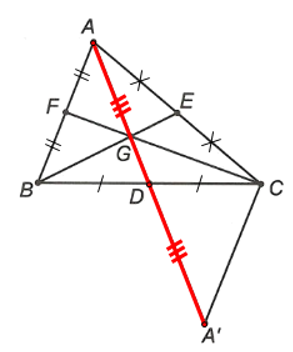
Ta xét đáp án A, B:
Vì G là trọng tâm của ∆ABC nên ta có và .
∆GBC có GB + GC > BC (bất đẳng thức tam giác).
Suy ra .
Do đó .
Khi đó (1).
Chứng minh tương tự ta được:
+) (2).
+) (3).
Lấy (1) + (2) + (3) vế theo vế, ta được: .
Suy ra .
Do đó .
Vậy đáp án A đúng, đáp án B sai.
Ta xét đáp án C:
Trên tia AD, lấy điểm A’ sao cho DA’ = DA.
Xét ∆ADB và ∆A’DC, có:
DA = DA’.
BD = CD (do AD là đường trung tuyến của ∆ABC).
(hai góc đối đỉnh).
Do đó ∆ADB = ∆A’DC (c.g.c).
Suy ra AB = A’C (cặp cạnh tương ứng).
Áp dụng bất đẳng thức tam giác cho ∆AA’C, ta được: AA’ < AC + A’C.
Suy ra AA’ < AC + AB hay 2AD < AC + AB (4).
Chứng minh tương tự, ta được:
+) 2BE < AB + BC (5).
+) 2CF < AC + BC (6).
Lấy (4) + (5) + (6) vế theo vế, ta được: 2AD + 2BE + 2CF < 2AC + 2AB + 2BC.
Suy ra 2(AD + BE + CF) < 2(AB + AC + BC).
Do đó AD + BE + CF < AB + AC + BC.
Vậy đáp án C đúng.
Vậy ta chọn đáp án D.
Đáp án đúng là: D
Ta xét đáp án A, B:
Vì G là trọng tâm của ∆ABC nên ta có và .
∆GBC có GB + GC > BC (bất đẳng thức tam giác).
Suy ra .
Do đó .
Khi đó (1).
Chứng minh tương tự ta được:
+) (2).
+) (3).
Lấy (1) + (2) + (3) vế theo vế, ta được: .
Suy ra .
Do đó .
Vậy đáp án A đúng, đáp án B sai.
Ta xét đáp án C:
Trên tia AD, lấy điểm A’ sao cho DA’ = DA.
Xét ∆ADB và ∆A’DC, có:
DA = DA’.
BD = CD (do AD là đường trung tuyến của ∆ABC).
(hai góc đối đỉnh).
Do đó ∆ADB = ∆A’DC (c.g.c).
Suy ra AB = A’C (cặp cạnh tương ứng).
Áp dụng bất đẳng thức tam giác cho ∆AA’C, ta được: AA’ < AC + A’C.
Suy ra AA’ < AC + AB hay 2AD < AC + AB (4).
Chứng minh tương tự, ta được:
+) 2BE < AB + BC (5).
+) 2CF < AC + BC (6).
Lấy (4) + (5) + (6) vế theo vế, ta được: 2AD + 2BE + 2CF < 2AC + 2AB + 2BC.
Suy ra 2(AD + BE + CF) < 2(AB + AC + BC).
Do đó AD + BE + CF < AB + AC + BC.
Vậy đáp án C đúng.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC có đường trung tuyến AD. Trên đoạn thẳng AD lấy hai điểm E, G sao cho AG = GE = ED. Trọng tâm của ∆ABC là điểm:
Cho ∆ABC có đường trung tuyến AD. Trên đoạn thẳng AD lấy hai điểm E, G sao cho AG = GE = ED. Trọng tâm của ∆ABC là điểm:
Câu 2:
Cho ∆ABC. Trên cạnh BC lấy điểm G sao cho BG = 2GC. Lấy điểm D sao cho C là trung điểm của AD. Gọi E là trung điểm BD. Khẳng định nào sau đây sai?
Cho ∆ABC. Trên cạnh BC lấy điểm G sao cho BG = 2GC. Lấy điểm D sao cho C là trung điểm của AD. Gọi E là trung điểm BD. Khẳng định nào sau đây sai?
Câu 3:
Cho ∆ABC có hai đường trung tuyến BD, CE cắt nhau tại G. Trên tia đối của tia DB, lấy điểm M sao cho DM = DG. Trên tia đối của tia EG lấy điểm N sao cho EN = EG. Khẳng định nào sau đây đúng nhất?
Câu 4:
Cho ∆ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Hãy so sánh GX, GY và GZ.
Cho ∆ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Hãy so sánh GX, GY và GZ.
Câu 5:
Cho ∆ABC cân tại A, có AM là đường trung tuyến. Khẳng định nào sau đây sai?
Cho ∆ABC cân tại A, có AM là đường trung tuyến. Khẳng định nào sau đây sai?
Câu 6:
Cho ∆ABC, đường trung tuyến AD. Trên tia đối của tia DA lấy điểm K sao cho . Qua B vẽ một đường thẳng song song với CK, cắt AC tại M. Gọi G là giao điểm của BM và AD. Khẳng định nào sau đây đúng?
Câu 7:
Cho ∆ABC có hai đường trung tuyến BE và CF cắt nhau tại G. Biết BE = CF. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC có hai đường trung tuyến BE và CF cắt nhau tại G. Biết BE = CF. Khẳng định nào sau đây đúng nhất?
Câu 9:
Cho ∆ABC, hai đường trung tuyến BM và CN cắt nhau tại G. Trên tia GB và GC lấy các điểm F và E sao cho G là trung điểm của FM, đồng thời là trung điểm của EN. Khẳng định nào sau đây sai?
Câu 10:
Cho ∆ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC cân tại A có hai đường trung tuyến BD và CE cắt nhau tại G. Khẳng định nào sau đây đúng nhất?
Câu 11:
Cho ∆ABC đều có ba đường trung tuyến AD, BE, CF cắt nhau tại G. Đoạn thẳng BE bằng với đoạn thẳng nào trong các đoạn thẳng sau:
Câu 12:
Cho ∆ABC, D là trung điểm của AC. Trên cạnh BD lấy điểm E sao cho BE = 2ED. Lấy điểm F thuộc tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK với AC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC, D là trung điểm của AC. Trên cạnh BD lấy điểm E sao cho BE = 2ED. Lấy điểm F thuộc tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là giao điểm của EK với AC. Khẳng định nào sau đây đúng nhất?
Câu 13:
Cho ∆ABC có hai đường trung tuyến BM, CN cắt nhau tại G.
So sánh tổng BM + CN và .
Cho ∆ABC có hai đường trung tuyến BM, CN cắt nhau tại G.
So sánh tổng BM + CN và .
Câu 14:
Cho ∆ABC có G là trọng tâm như hình bên.
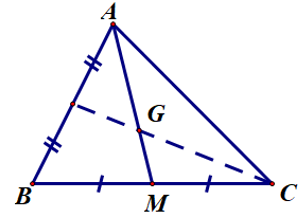
Tìm x, biết AG = 4x + 6 và AM = 9x.
Cho ∆ABC có G là trọng tâm như hình bên.
Tìm x, biết AG = 4x + 6 và AM = 9x.


