Bài giảng Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
Kiến thức cần nhớ
1. Vị trí tương đối của hai đường thẳng trong không gian.
Cho hai đường thẳng a và b trong không gian. Khi đó có thể xảy ra một trong các trường hợp sau:
- Trường hợp 1. Có một mặt phẳng chứa a và b.
Khi đó, ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng có 3 khả năng xảy ra:
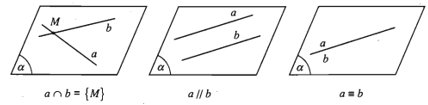
i) a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và kí hiệu . Ta có thể viết .
ii) a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.
iii) a trùng b, kí hiệu là .
- Trường hợp 2. Không có mặt phẳng nào chứa a và b.
Khi đó ta nói a và b chéo nhau hay a chéo với b.
- Ví dụ 1. Cho tứ diện ABCD. Hãy chỉ ra các cặp đường thẳng chéo nhau.
Lời giải:
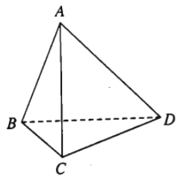
Đường thẳng AB và CD chéo nhau.
Đường thẳng AC và BD chéo nhau.
Đường thẳng AD và BC chéo nhau.
2. Tính chất
- Định lí. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
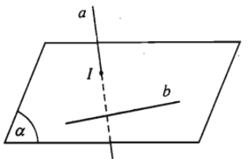
- Định lí (về giao tuyến của ba mặt phẳng).
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
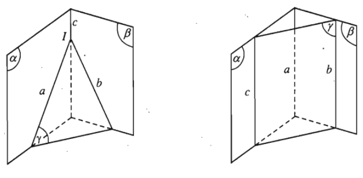
- Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
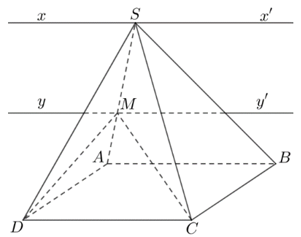
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của các mặt phẳng:
a) (SAD) và (SBC).
b) (MCD) và (SAB), với M là một điểm bất kì thuộc cạnh SA.
Lời giải:
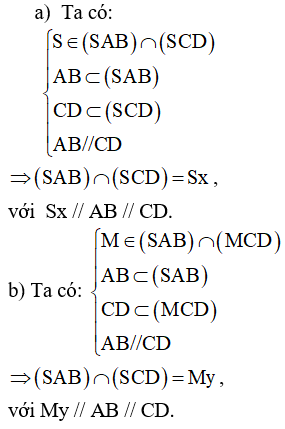
- Định lí. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Ta có: a // c; b // c nên a // b hay a // b // c (ba đường thẳng song song).
Ví dụ 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng IJ // AB, từ đó suy ra IJ // CD.
Lời giải:
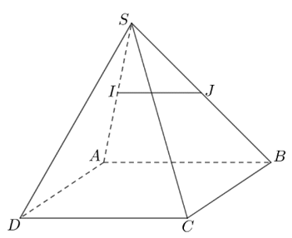
Xét tam giác SAB có I, J lần lượt là trung điểm của các cạnh SA, SB nên IJ là đường trung bình của tam giác SAB.
Từ đó suy ra IJ // AB.
Lại có AB // CD (vì ABCD là hình bình hành) nên từ đó ta có IJ // CD (vì cùng song song với đường thẳng AB).
3. Phương pháp giải
Dựng đường thẳng chứa a và song song với b (hoặc đường thẳng chứa b và song song với a) để tính khoảng cách giữa hai đường thẳng chéo nhau.
Khảo sát khối chóp đỉnh S có đường cao SH, yêu cầu tính khoảng cách giữa 2 đường thẳng chéo nhau d (thuộc mặt đáy) và đường thẳng SC thuộc mặt bên của khối chóp trong trường hợp d không vuông góc với SC.
Dựng hình: Tìm giao điểm C của cạnh bên SC và mặt đáy (giao điểm của cạnh thuộc mặt bên và mặt đáy). Từ C ta dựng đường thẳng
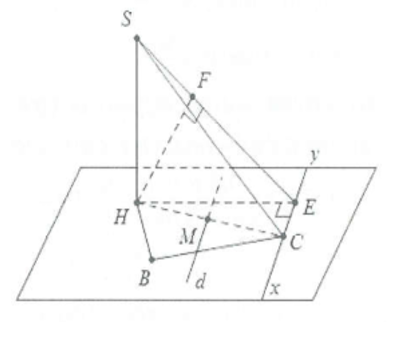
Khi đó d(d;SC) = d(d;(Sxy))
Gọi
Ta có:
Chú ý: Để tính d(d;(Sxy)) ta có thể lấy bất kỳ điểm nào thuộc d (không nhất thiết là điểm M) sao cho việc quy đổi khoảng cách cần tìm về khoảng cách từ chân đường cao H đến mặt phẳng (Sxy) dễ dàng nhất.
Bài tập tự luyện (có đáp án)
Bài 1: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có AB = a, . Biết
a) Tính khoảng cách giữa hai đường thẳng SB và AC
b) Tính khoảng cách giữa hai đường thẳng SC và AB.
Lời giải
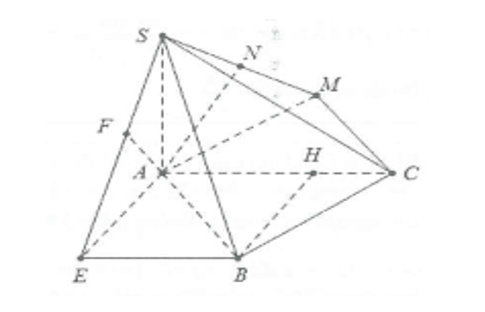
a) Dựng
Dựng
Dựng dễ thấy
Ta có:
b) Dựng
Dựng
Lại có :
(Xem thêm các bài tập khác trong file đím kèm)
Xem thêm các dạng bài tập liên quan khác:
70 Bài tập về hai đường thẳng chéo nhau (có đáp án năm 2024)
70 Bài tập về hai đường thẳng song song (có đáp án năm 2023)
70 Bài tập về hai đường thẳng vuông góc (có đáp án năm 2023)
90 Bài tập về Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách (2024) có đáp án
100 Bài tập về đường thẳng vuông góc với mặt phẳng (có đáp án năm 2023)












