Bài giảng Toán 8 Bài 2: Định lí đảo và hệ quả của định lí Ta – lét
Kiến thức cần nhớ
1. Định lý đảo
- Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
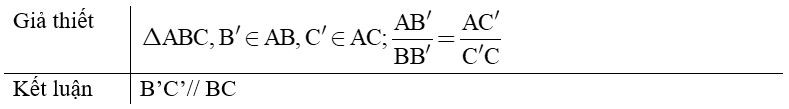
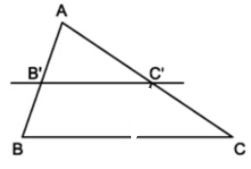
Ví dụ 1. Trong tam giác ABC có AB = 10cm; AC = 15cm. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 6cm. Chứng minh B’C’// BC.
Lời giải:
Ta có: B’B = AB – AB’ = 10 – 4 = 6cm,
Và CC’ = AC – AC’ = 15 – 6 = 9 cm
Ta có:
AB'BB'=46=23; AC'CC'=69=23⇒AB'BB'=AC'CC'
Theo định lí ta – lét đảo, suy ra: B’C’ // BC.
2. Hệ quả của định lý Ta – lét
- Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
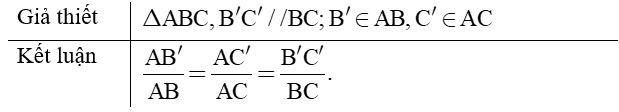
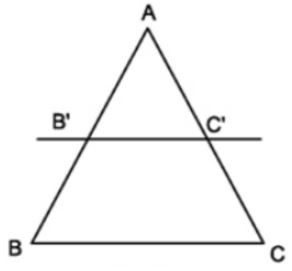
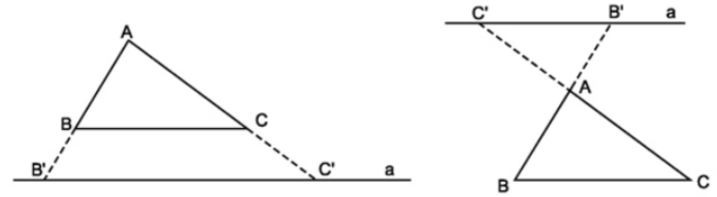
- Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.
Ví dụ 2. Trong tam giác ABC có AB = 6cm và B’C’// BC. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 3cm. Tính độ dài cạnh AC.
Lời giải:
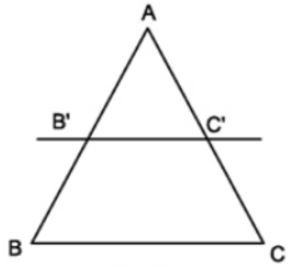
Áp dụng hệ quả trên ta có:
AB'AB=AC'AC=B'C'BC
Khi đó ta có:
AB'AB=AC'AC⇔46=3AC⇒AC=6.34=92(cm)
Các dạng toán về định lí đảo và hệ quả của định lí Ta - lét
Dạng 1. Tính độ dài đoạn thẳng. Chia đoạn thẳng cho trước thành các phần bằng nhau.
1. Tính độ dài đoạn thẳng:
+ Xác định đường thẳng song song với một cạnh của tam giác.
+ Áp dụng hệ quả của định lí Ta-lét để lập tỉ lệ thức của các đoạn thẳng.
+ Thay số vào hệ thức rồi giải phương trình.
2. Chia đoạn thẳng cho trước thành các phần bằng nhau cách sử dụng hệ quả của định lí Ta-lét hoặc tính chất của đường thẳng song song cách đều.
Dạng 2. Chứng minh hệ thức hình học.
+ Xác định đường thẳng song song với một cạnh của tam giác.
+ Áp dụng hệ quả của định lí Ta-lét để lập tỉ lệ thức của các đoạn thẳng.
+ Sử dụng các tính chất của tỉ lệ thức hoặc cộng hay nhân theo vế các đẳng thức hình học.
Dạng 3. Chứng minh hai đường thẳng song song.
+ Sử dụng định lí Ta-lét, lập tỉ lệ thức giữa các đoạn thẳng.
+ Áp dụng định lí Ta-lét đảo, kết luận hai đường thẳng song song.
Dạng 4. Vẽ thêm đường thẳng song song để chứng minh hệ thức hình học, tính tỉ số hai đoạn thẳng.
+ Vẽ thêm đường thẳng song song.
+ Áp dụng hệ quả của định lí Ta-lét để lập tỉ lệ thức giữa các đoạn thẳng.
+ Biến đổi tỉ lệ thức.
Bài tập tự luyện
1. Bài tập vận dụng
Bài 1. Tính x trong hình vẽ sau, biết FG// HT
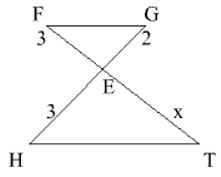
Lời giải:
Áp dụng hệ quả của định lí Ta – lét với FG// HT ta có:
EFET=EGHE⇔ET=EF.HEEG=3.32=4,5
Vậy x = 4,5.
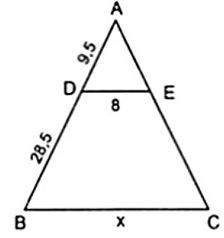
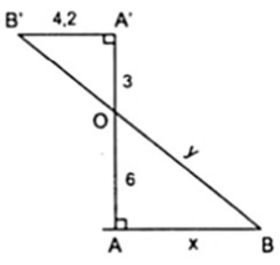
Bài 2. Tính độ dài x, y trong các hình sau biết DE // BC
a)
b)
Lời giải:
a) Áp dụng hệ quả của định lí Ta – lét ta có:
BCDE=ABAD hay x8=28,5+9,59,5=389,5
⇔x=8.389,5=32
Vậy x = 32.
b) Ta có: A’B’// AB vì cùng vuông góc AA’.
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'∥AB⇒ABA'B'=AOA'O'
hay x4,2=63⇔x=8,4
Áp dụng định lí Py – ta – go với tam giác OAB ta có:
OB2=AB2+OA2⇒y=√8,42+62≈10,32
Vậy x=8,4 và y≈10,32.
Bài 3. Cho tam giác ABC, một đường thẳng d cắt 2 cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 5cm, AN = 6 cm và AC = 13,5cm; BC = 12 cm. Tính MN?
Lời giải:
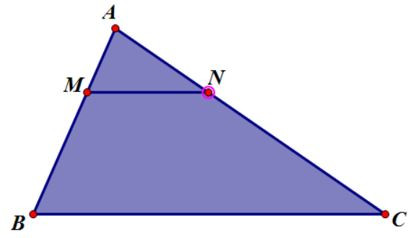
Do N nằm giữa A và C nên:
NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có: AMMB=ANNC (45=67,5)
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta - let ta có;
ANAC=MNBC⇒MN=AN.BCAC=6.1213,5=163cm
Bài 4. Cho tam giác ABC, đường thẳng d song song với BC cắt 2 cạnh AB và AC lần lượt tại M và N. Biết rằng AMMB=12. Tỉnh tỉ số chu vi tam giác AMN và ABC?
Lời giải:
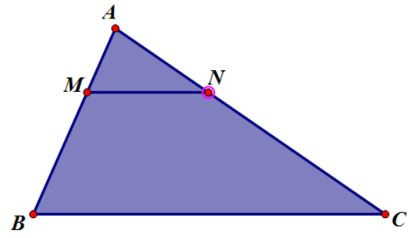
Ta có: AMMB=12⇒AMMB+AM=12+1⇒AMAB=13
Vì MN// BC nên theo hệ quả định lí Ta let ta có:
AMAB=ANAC=MNBC=13
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
AMAB=ANAC=MNBC=AM+AN+MNAB+AC+BC=13
Do đó, tỉ số chu vi tam giác AMN và ABC là 13












