50 Bài tập Ôn tập chương 2 (có đáp án năm 2023) - Toán 9

Kiến thức cần nhớ 

1. Khái niệm hàm số

• Nếu đại lượng y phụ thuộc vào một đại lượng x thay đổi sao cho mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số

• Hàm số có thể được cho bằng bảng hoặc bằng công thức, ...

• Hàm số thường được ký hiệu bởi những chữ f, g, h, ... chẳng hạn khi y là hàm số của biến số x, ta viết y = f(x) hoặc y = g(x), ….

• f(a) là giá trị của hàm số y = f(x) tại x = a. Khi hàm số y được cho bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính trong biểu thức.

• Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.

2. Đồ thị của hàm số

Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y = f(x).

3. Hàm số đồng biến, nghịch biến

Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc .

• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến).

• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng giảm đi thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).

Nói cách khác, cho hàm số y = f(x) xác định trên tập số thực R. Với $x_1,x_2\in R$ ta có:

+ Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số đồng biến.

+ Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số nghịch biến.

4. Định nghĩa hàm số bậc nhất

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0.

Chú ý: Khi b = 0 ta có hàm số y = ax (đã học ở lớp 7).

5. Tính chất hàm số bậc nhất

Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có các tính chất như sau:

• Đồng biến trên R khi a > 0.

• Nghịch biến trên R khi a < 0.

6. Đồ thị hàm số y = ax + b (a ≠ 0)

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

- Cắt trục tung tại điểm có tung độ bằng b.

- Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0

Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.

7. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).

• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì $x=\frac{-b}{a}$, ta được điểm $Q\left(-\frac{b}{a};0\right)$ thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).

 Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.

8. Đường thẳng song song

Hai đường thẳng y = ax + b (a ≠ 0) và y = a'x + b' (a' ≠ 0) song song với nhau khi và chỉ khi a = a', b ≠ b' và trùng nhau khi và chỉ khi a = a', b = b'.

9. Đường thẳng cắt nhau

Hai đường thẳng y = ax + b (a ≠ 0) và y = a'x + b' (a' ≠ 0) cắt nhau khi và chỉ khi a ≠ a'.

Chú ý. Khi a ≠ a' và b = b' thì hai đường thẳng có cùng tung độ gốc, do đó chúng cắt nhau tại một điểm trên trục tung có tung độ là b.

10. Khái niệm hệ số góc của đường thẳng y = ax + b (a ≠ 0)

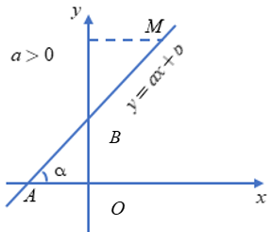
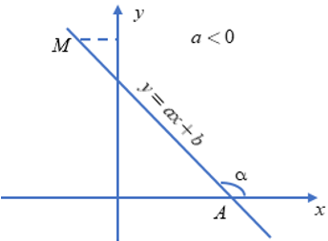
a. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) với trục Ox

Gọi A là giao điểm của đường thẳng y = ax + b với trục Ox và M là một điểm thuộc đường thẳng và có tung độ dương.

Khi đó, $\widehat{Max}$ là góc tạo bởi đường thẳng y = ax + b với trục Ox.

11. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

− Các đường thẳng có cùng hệ số a (a là hệ số của x) thì tạo với trục Ox các góc bằng nhau.

Khi a > 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn 90°.

Khi a < 0 góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù và nếu a càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn 180°.

Như vậy, góc tạo bởi đường thẳng y = ax + b và trục Ox phụ thuộc vào a.

Người ta gọi a là hệ số góc của đường thẳng y = ax + b.

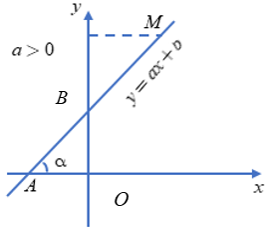
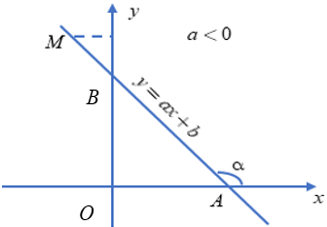
Chú ý. Khi b = 0, ta có hàm số y = ax. Trong trường hợp này, ta có thể nói a là hệ số góc của đường thẳng y = ax.

Bài tập tự luyện 

Bài 1: Tìm số a, biết đồ thị hàm số y = 2x² – ax – 1 đi qua điểm M(2; 3).

Lời giải:

Vì đồ thị hàm số y = 2x² – ax – 1 đi qua điểm M(2; 3) nên:

2 . 2² – a . 2 – 1 = 3

$\iff$ 8 – 2a – 1 = 3

$\iff$ 7 – 2a = 3

$\iff$ 2a = 4

$\iff$ a = 2.

Vậy với a = 2 thì đồ thị hàm số đi qua M(2; 3).

Bài 2: Cho hàm số f(x) = x³ – 3x + 5. Hãy tính f(−1); $f\left(\frac{2}{3}\right)$; $f\left(\frac{-1}{2}\right)$.

Lời giải:

Ta có: f(−1) = (−1)³ – 3. (−1) + 5 = −1 + 3 + 5 = 7;

$$\begin{gathered} f\left(\frac{2}{3}\right)={\left(\frac{2}{3}\right)}^3-3\cdot \frac{2}{3}+5 \\ =\frac{8}{27}-2+5=\frac{89}{27}; \end{gathered}$$

$$\begin{gathered} f\left(-\frac{1}{2}\right)={\left(\frac{-1}{2}\right)}^3-3\cdot \left(\frac{-1}{2}\right)+5 \\ =\frac{-1}{8}+\frac{3}{2}+5 \end{gathered}$$

$=\frac{-1}{8}+\frac{12}{8}+\frac{40}{8}=\frac{51}{8}.$

Vậy f(−1) = 7; $f\left(\frac{2}{3}\right)=\frac{89}{27}$; $f\left(\frac{-1}{2}\right)=\frac{51}{8}$.

Bài 3: Cho hàm số f(x) = 4x² – 5x + 2. Các điểm A(0; 2), B(−l; 4), C(1; 1) có thuộc đồ thị hàm số không? Tại sao?

Lời giải:

Vì f(0) = 4 . 0 – 5 . 0 + 2 = 2 nên điểm A(0 ; 2) thuộc đồ thị hàm số đã cho.

Vì f(−1) = 4 . 1 + 5 . 1 + 2 = 11 nên điểm B(−1 ; 4) không thuộc đồ thị hàm số đã cho.

Vì f(1) = 4 . 1 – 5 . 1 + 2 nên điểm C(1; 1) thuộc đồ thị hàm số đã cho.

Vậy điểm A(0; 2), C(1; 1) thuộc đồ thị hàm số và điểm B(−l; 4) không thuộc đồ thị hàm số đã cho.

Bài 4: Cho hàm số y = ax + 1. Biết đồ thị hàm số đi qua điểm A(1; 2). Tìm giá trị của a.

Lời giải

Đồ thị hàm số đi qua điểm A(1; 2) nên ta có:

2 = a . 1 + 1

$\iff$ a + 1 = 2

$\iff$ a = 1.

Vậy với a = 1 thì đồ thị hàm số đi qua A(1; 2).

Bài 5: Cho hai hàm số f(x) = 5x – 3 và g(x) = − 4x +1. Tính:

a) $f(-2)-g\left(\frac{1}{2}\right)$;

b) 2f ²(–3) – 3g³(–2).

Lời giải

a) Ta có: f(−2) = 5. (−2) – 3 = –10 – 3 = –13;

$$\begin{gathered} g\left(\frac{1}{2}\right)=(-4).\frac{1}{2}+1 \\ =-2+1=-1 \end{gathered}$$

Do đó $f(-2)-g\left(\frac{1}{2}\right)$ = –13 – (–1) = –13 + 1 = –12.

Vậy $f(-2)-g\left(\frac{1}{2}\right)=-12$

b) f(−3) = 5. (−3) – 3 = –15 – 3 = –18;

g(−2) = (−4) . (−2) + 1 =8 + 1 = 9.

2f ²(–3) – 3g³(–2) = 2 . (–18)² – 3 . 9³

= 2 . 324 – 3. 729 = 648 − 2187 = −1539.

Vậy 2f ²(–3) – 3g³(–2) = −1539.

Bài 6: Cho các hàm số y = 2mx + m + 1 (1) và hàm số y = (m − 1)x + 3 (2). Xác định m để hàm số (1) đồng biến, hàm số (2) nghịch biến.

Lời giải:

Để hàm số (1) đồng biến, hàm số (2) nghịch biến thì m thỏa mãn:

− Hàm số (1) đồng biến (tức a > 0) hay 2m > 0 $\iff$ m > 0 (1)

− Hàm số (2) nghịch biến (tức a < 0) hay m − 1 < 0 $\iff$ m < 1 (2)

Từ (1) và (2) suy ra: 0 < m < 1.

Vậy để hàm số (1) đồng biến và hàm số (2) nghịch biến thì m thỏa mãn: 0 < m < 1.

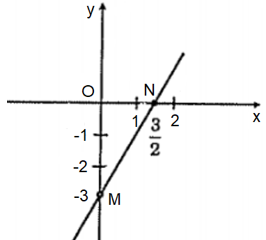
Bài 7: Vẽ đồ thị hàm số y = 2x – 3.

Lời giải:

Vẽ đồ thị hàm số y = 2x – 3.

Bước 1: Cho x = 0 thì y = −3, ta được điểm M(0; −3) ∈ Oy.

Cho y = 0 thì x = 2x – 3 = 0 $\iff x=\frac{3}{2}$, ta được điểm $N\left(\frac{3}{2};0\right)$.

Bước 2: Vẽ đường thẳng đi qua hai điểm M và N, ta được đồ thị hàm số y = 2x – 3.

Ta có đồ thị hàm số:

Bài 8: Cho tọa độ hai điểm $A\left(\frac{-1}{3};5\right);B\left(\frac{5}{2};2\right)$.

Hỏi điểm nào thuộc đồ thị hàm số y = − 3x + 4?

Lời giải:

* Với $A\left(\frac{-1}{3};5\right)$: Thay $x_A=\frac{-1}{3}$ vào hàm số y = − 3x + 4.

Ta được: $y=(-3).\frac{-1}{3}+4=1+4=5$.

Do đó, điểm $A\left(\frac{-1}{3};5\right)$ thuộc đồ thị hàm số y = − 3x + 4.

* Với $B\left(\frac{5}{2};2\right)$: Thay $x_A=\frac{5}{2}$ vào hàm số y = − 3x + 4.

Ta được: $y=(-3).\frac{5}{2}+4=\frac{-15}{2}+4=\frac{-7}{2}$ ≠ 2.

Do đó, điểm $B\left(\frac{5}{2};2\right)$ không thuộc đồ thị hàm số y = − 3x + 4.

Vậy điểm $A\left(\frac{-1}{3};5\right)$ thuộc đồ thị hàm số y = − 3x + 4.

Bài 9: Cho hàm số y = (3 – 2m)x + 4m – 4 (1)

a) Tìm m để (1) là hàm số đồng biến trên R.

b) Tìm m để đồ thị hàm số (1) song song với đường thẳng y = 3x – 5.

Lời giải:

a) Hàm số (1) đồng biến trên R khi và chỉ khi:

3 – 2m > 0

$\iff$ −2m > −3

$\iff$ m < $\frac{3}{2}$.

b) Đồ thị hàm số (1) song song với đường thẳng y = 3x – 5 khi:

$$\begin{gathered} \left\{\begin{array}{l}3-2m=3\\ 4m-3\ne -5\end{array}\right. \\ \iff \left\{\begin{array}{l}m=0\\ m\ne \frac{-1}{2}\end{array}\right. \\ \iff m=0 \end{gathered}$$

Vậy đồ thị hàm số (1) song song với đường thẳng y = 3x – 5 thì m = 0.

Bài 10: Viết phương trình đường thẳng song song với đường thẳng (d) : y = $\frac{1}{2}$x + 1 và đi qua điểm M(2 ; −5).

Lời giải:

Gọi phương trình đường thẳng cần tìm là (d’): y = ax + b.

Vì d // d’ nên a = $\frac{1}{2}$.

Ta có (d’): y = $\frac{1}{2}$x + b (b ≠ 1).

Mặt khác vì (d’) đi qua điểm M(2 ; −5) nên −5 = $\frac{1}{2}$. 2 + b.

Do đó b = −6.

Vậy phương trình đường thẳng cần tìm là y = $\frac{1}{2}$x – 6.

Bài 11: Viết phương trình đường thẳng

a) Đi qua hai điểm A(−2 ; −5) và B(1 ; 4);

b) Đi qua điểm M(6 ; 2) và vuông góc với đường thẳng y = $\frac{-1}{3}x$ + 1.

Lời giải:

a) Gọi phương trình đường thẳng AB là y = ax + b.

Vì đường thẳng đi qua A (−2; −5) nên −5 = −2a + b.

Do đó b = 2a – 5.

Vì đường thẳng đi qua B (1; 4) nên 4 = a + b.

Do đó b = 4 – a.

Từ đó: 2a – 5 = 4 – a nên 3a = 9.

Suy ra a = 3; b = 1.

Vậy phương trình đường thẳng AB là y = 3x + 1.

b) Gọi phương trình đường thẳng cần tìm là y = ax +b.

Vì đường thẳng này vuông góc với đường thẳng y = $\frac{-1}{3}$x + 1 nên $\frac{-1}{3}$. a = −1.

Do đó a = 3.

Vì đường thẳng đi qua điểm M(6 ; 2) nên:

2 = 3.6 + b $\iff$ b = −16.

Vậy phương trình đường thẳng cần tìm là y = 3x – 16.

Bài 12: Viết phương trình đường thẳng (d) đi qua điểm M(1; 2) và có hệ số góc là 3.

Lời giải:

Phương trình đường thẳng có hệ số góc 3 (tức là a = 3) có phương trình dạng:

y = 3x + b.

Vì phương trình này đi qua điểm M(1; 2) nên có:

2 = 3.1 + b

$\iff$ b = 2 − 3

$\iff$ b = −1.

Vậy phương trình đường thẳng cần tìm là: y = 3x – 1.

Bài 13:

a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1).

b) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1; −2).

Lời giải

Đường thẳng đi qua gốc tọa độ có dạng y = ax + b.

a) Vì đường thẳng y = ax đi qua điểm A(2; 1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.

Ta có: 1 = a . 2 $\iff$ a = $\frac{1}{2}$.

Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1) là a = $\frac{1}{2}$.

b) Vì đường thẳng y = ax đi qua điểm B(1; −2) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.

Ta có: − 2 = a . 1 $\iff$ a = − 2.

Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1; − 2) là a = − 2.

Bài 14: Xác định hàm số y = ax + b biết đồ thị hàm số đi qua điểm A(4; 0) và B(0; 3). Khi đó, hãy tính:

a) Vẽ đồ thị hàm số (d) vừa tìm được và tính góc α tạo bởi đường thẳng (d) và trục Ox.

b) Khoảng cách từ gốc tọa độ O đến đường thẳng (d).

c) Tính diện tích tam giác OAB.

Lời giải:

a) Vì (d) đi qua A(4; 0) nên tọa độ A phải thỏa mãn phương trình:

y = ax + b

$\iff$ 4a + b = 0 (1)

Tương tự (d) đi qua B(0; 3) nên tọa độ B phải thỏa mãn phương trình:

y = ax + b

$\iff$ 3 = a . 0 + b

$\iff$ b = 3.

Thay b = 3 vào (1) ta được a = $-\frac{3}{4}$.

Do đó đồ thị hàm số tìm là: $y=-\frac{3}{4}x+3$.

* Vẽ đồ thị hàm số

+ Cho x = 0 thì y = 3 ta được điểm A(4; 0).

+ Cho y = 0 thì x = 4 ta được điểm B(0; 3).

Do đó, đồi thị hàm số đi qua 2 điểm A(4; 0) và B(0; 3).

Ta có đồ thị như sau:

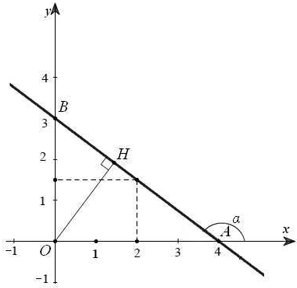
− Xét tam giác AOB vuông tại O, ta có:

 $\tan \widehat{OAB}=\frac{OB}{OA}=\frac{3}{4}\approx \tan {36}^{o}52\text{'}$

$\Rightarrow \widehat{OAB}\simeq {36}^{o}52\text{'}$

$\Rightarrow \alpha ={180}^o-{36}^{o}52\text{'}={143}^{o}8\text{'}$

Vây góc tạo bởi (d) và trục hoành Ox (tức đường thẳng y = 0) là α = 143^o8'.

b) Vẽ OH ⊥ AB.

Tam giác OAB là tam giác vuông tại O, ta có OH ⊥ AB nên:

$$\begin{gathered} \frac{1}{O{H}^2}=\frac{1}{O{A}^2}+\frac{1}{O{B}^2} \\ =\frac{1}{4^2}+\frac{1}{3^2}=\frac{25}{144} \end{gathered}$$

$\Rightarrow OH=\sqrt{\frac{144}{25}}=\frac{12}{5}=\mathrm{2,4}$.

Vậy khoảng cách từ gốc tọa độ O tới đường thẳng (d) là 2,4 (đvđd).

c) Vì tam giác OAB là tam giác vuông tại O nên ta có:

$S_{OAB}=\frac{1}{2}OA.OB=\frac{1}{2}.4.3=6$.

Vậy diện tích tam giác OAB là 6 (đvdt).