50 Bài tập Ôn tập chương 1 (có đáp án năm 2023) - Toán 9

Kiến thức cần nhớ 

1. Căn bậc hai

a. Khái niệm: Căn bậc hai của một số a không âm là số x sao cho x² = a.

b. Tính chất:

- Số âm không có căn bậc hai.

- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết $\sqrt{0}=0$.

- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là $\sqrt{a}$, số âm ký hiệu là $-\sqrt{a}$.

2. Căn bậc hai số học

a. Định nghĩa: Với số dương a, số $\sqrt{a}$ được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.

Chú ý. Với a ≥ 0, ta có:

Nếu $x=\sqrt{a}$ thì x ≥ 0 và x² = a;

Nếu x ≥ 0 và x² = a thì $x=\sqrt{a}$.

- Ta viết $x=\sqrt{a}\iff \left\{\begin{array}{l}x\ge \mathrm{0,}\\ x^2=a.\end{array}\right.$

b. Phép khai phương:

- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).

- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.

3. So sánh các căn bậc hai số học

Định lí. Với hai số a và b không âm, ta có: $a<b\iff \sqrt{a}<\sqrt{b}$.

4. Căn thức bậc hai

Với A là một biểu thức đại số, người ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.

$\sqrt{A}$ xác định(có nghĩa) khi A lấy giá trị không âm.

5. Hằng đẳng thức $\sqrt{A^2}=\left|A\right|$

Định lí. Với mọi số a, ta có $\sqrt{a^2}=\left|a\right|$.

Chú ý. Một cách tổng quát, với A là một biểu thức ta có $\sqrt{A^2}=\left|A\right|$, có nghĩa là:

$\sqrt{A^2}=A$ nếu A ≥ 0 (tức là A lấy giá trị không âm);

$\sqrt{A^2}=-A$ nếu A < 0 (tức là A lấy giá trị âm).

6. Căn bậc hai của một tích

Định lí. Với hai số a và b không âm, ta có $\sqrt{a.b}=\sqrt{a}.\sqrt{b}$.

Chú ý: Định lí trên có thể mở rộng cho tích của nhiều số không âm.

7. Quy tắc khai phương một tích

Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả lại với nhau.

$\sqrt{a.b}=\sqrt{a}.\sqrt{b}$ (với a, b ≥ 0).

8. Quy tắc nhân các căn bậc hai

Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới căn với nhau rồi khai phương kết quả đó.

$\sqrt{a}.\sqrt{b}=\sqrt{a.b}$ (với a, b ≥ 0).

Chú ý. Một cách tổng quát, với hai biểu thức A và B không âm ta có:

$\sqrt{A.B}=\sqrt{A}.\sqrt{B}$.

Đặc biệt, với biểu thức A không âm ta có: ${\left(\sqrt{A}\right)}^2=\sqrt{A^2}=A$.

9. Căn bậc hai của một thương

Định lí. Với số a không âm và số b dương, ta có: $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$.

10. Quy tắc khai phương một thương

Muốn khai phương một thương $\frac{a}{b}$, trong đó số a không âm và số b dương, ta có thể lần lượt khai phương của các số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.

$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ (với a ≥ 0, b > 0).

11. Quy tắc chia hai căn bậc hai

Muốn chia hai căn bậc hai của số a không âm và số b dương, ta có thể lấy số a chia cho số b rồi khai phương kết quả vừa tìm được.

$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$ (với a ≥ 0, b > 0).

Chú ý. Một cách tổng quát, với biểu thức A không âm và biểu thức B dương, ta có: $\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}$.

12. Giới thiệu bảng căn bậc hai

+ Bảng được chia thành các hàng và các cột.

+ Căn bậc hai của các số được viết bởi không qua ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9.

+ Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.

+ Bảng căn bậc hai.

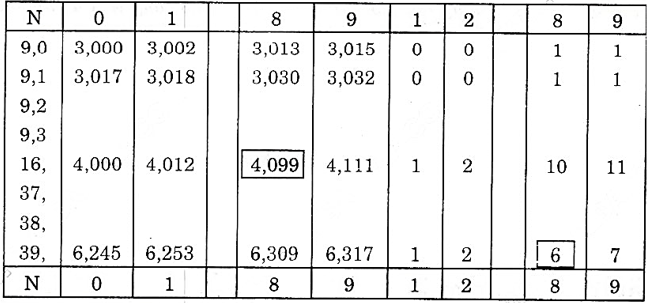
13. Đưa một thừa số ra ngoài dấu căn

• Với a ≥ 0, b ≥ 0, ta có: $\sqrt{a^{2}b}=a\sqrt{b}$. Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.

• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.

• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.

Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có $\sqrt{A^2.B}=\left|A\right|\sqrt{B}$, tức là:

Nếu A ≥ 0 và B ≥ 0 thì $\sqrt{A^{2}B}=A\sqrt{B}$;

Nếu A < 0 và B ≥ 0 thì $\sqrt{A^{2}B}=-A\sqrt{B}$.

14. Đưa thừa số vào trong dấu căn

• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.

Với A ≥ 0 và B ≥ 0 thì $A\sqrt{B}=\sqrt{A^{2}B}$.

Với A < 0 và B ≥ 0 thì $A\sqrt{B}=-\sqrt{A^{2}B}$.

• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.

15. Khử mẫu của biểu thức lấy căn

Tổng quát: Với các biểu thức A, B mà A.  B ≥ 0 và B ≠ 0, ta có:

$\sqrt{\frac{A}{B}}=\frac{\sqrt{AB}}{\left|B\right|}$.

16. Trục căn thức ở mẫu

Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.

Tổng quát:

• Với các biểu thức A, B mà B > 0 ta có: $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}$.

• Với các biểu thức A, B, C mà A ≥ 0, A ≠ B², ta có:

$\frac{C}{\sqrt{A}\pm B}=\frac{C(\sqrt{A}\mp B)}{A-B^2}$.

• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:

$\frac{C}{\sqrt{A}\pm \sqrt{B}}=\frac{C(\sqrt{A}\mp \sqrt{B})}{A-B}$.

17. Rút gọn biểu thức chứa căn thức bậc hai

- Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.

- Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thứa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ.

18. Khái niệm căn bậc ba

Định nghĩa: Căn bậc ba của một số thực a là số x sao cho x³ = a.

• Mỗi số a đều có duy nhất một căn bậc ba.

• Căn bậc ba của một số a được kí hiệu là $x=\sqrt[3]{a}$ (số 3 gọi là chỉ số căn).

• Phép lấy căn bậc ba của một số gọi là phép khai căn bậc ba.

Chú ý. Từ định nghĩa căn bậc ba, ta có ${\left(\sqrt[3]{a}\right)}^3=\sqrt[3]{a^3}=a$.

Nhận xét: 

- Căn bậc ba của số dương là số dương;

- Căn bậc ba của số âm là số âm;

- Căn bậc ba của số 0 là số 0.

19. Tính chất căn bậc ba

• a < b Û $\sqrt[3]{a}<\sqrt[3]{b}$.

• $\sqrt[3]{ab}=\sqrt[3]{a}.\sqrt[3]{b}$.

• Với b ≠ 0, ta có: $\sqrt[3]{\frac{a}{b}}=\frac{\sqrt[3]{a}}{\sqrt[3]{b}}$.

Bài tập tự luyện 

Bài 1. Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng:

25; 196; 289; 484.

Lời giải:

- Căn bậc hai số học của 25 là 5 nên 25 có hai căn bậc hai là 5 và −5;

- Căn bậc hai số học cuả 196 là 14 nên 196 có hai căn bậc hai là 14 và −14;

- Căn bậc hai số học của 289 là 17 nên 289 có hai căn bậc hai là 17 và −17;

- Căn bậc hai số học cuả 484 là 22 nên 484 có hai căn bậc hai là 22 và −22.

Bài 2. So sánh:

a) 4 và $\sqrt{26}$;

b) 8 và $\sqrt{31}$.

Lời giải:

a) Vì 16 < 26 nên $\sqrt{16}<\sqrt{26}$.

Vậy $4<\sqrt{26}$.

b) Vì 64 > 31 nên $\sqrt{64}>\sqrt{31}$.

Vậy $8>\sqrt{31}$.

Bài 3. Tìm số x không âm, biết:

a) $\sqrt{x}=18$;

b) $3\sqrt{x}=24$;

c) $\sqrt{x}<\sqrt{5}$;

d) $\sqrt{2x}<6$.

Lời giải:

a) $\sqrt{x}=18$

Vì x ≥ 0 nên bình phương hai vế ta được:

x = 18² 

$\iff$ x = 324.

Vậy x = 324.

b) $3\sqrt{x}=24$

$\iff \sqrt{x}=8$

Vì x ≥ 0 nên bình phương hai vế ta được:

x = 8² 

$\iff$ x = 64.

Vậy x = 64.

c) $\sqrt{x}<\sqrt{5}$

Vì x ≥ 0 nên bình phương hai vế ta được: x < 5.

Vậy 0 ≤ x < 5.

d) $\sqrt{2x}<6$

Vì x ≥ 0 nên bình phương hai vế ta được:

2x < 36

$\iff$ x < 18.

Vậy 0 ≤ x < 18.

Bài 4. Với giá trị nào của a thì mỗi căn thức sau có nghĩa:

a) $\sqrt{\frac{a}{4}}$;

b) $\sqrt{-3a}$;

c) $\sqrt{2a+9}$.

Lời giải:

a) Điều kiện xác định: $\frac{a}{4}\ge 0\iff a\ge 0$.

Vậy với a ≥ 0 thì $\sqrt{\frac{a}{4}}$ có nghĩa.

b) Điều kiện xác định: − 3a ≥ 0 ⇔ a ≤ 0.

Vậy với a ≤ 0 thì $\sqrt{-3a}$ có nghĩa.

c) Điều kiện xác định: 2a + 9 ≥ 0 $\iff a\ge \frac{-9}{2}$.

Vậy với $a\ge \frac{-9}{2}$ thì $\sqrt{2a+9}$ có nghĩa.

Bài 5. Rút gọn các biểu thức sau:

a) $\sqrt{{(3-\sqrt{6})}^2}$;

b) $3\sqrt{a^2}$ với a ≥ 0;

c) $5\sqrt{{(a-3)}^2}$ với a < 3.

Lời giải:

a) $\sqrt{{(3-\sqrt{6})}^2}=\left|3-\sqrt{6}\right|=3-\sqrt{6}$.

Ta có $3=\sqrt{9}$ mà $\sqrt{9}>\sqrt{6}$ nên $3-\sqrt{6}>0$.

Do đó $\left|3-\sqrt{6}\right|=3-\sqrt{6}$.

Vậy $\sqrt{{(3-\sqrt{6})}^2}=3-\sqrt{6}$.

b) $3\sqrt{a^2}=3\left|a\right|$.

Vì a ≥ 0 nên 3|a| = 3a.

Vậy $3\sqrt{a^2}=3a$.

c) $5\sqrt{{(a-3)}^2}=5\left|a-3\right|$.

Vì a < 3 nên a – 3 < 0.

Do đó 5|a – 3| = 5(3 – a) = 15 – 5a.

Vậy $5\sqrt{{(a-3)}^2}=15-5a$.

Bài 6. Tìm x, biết:

a) $\sqrt{x^2}=15$;

b) $\sqrt{9x^2}=12$;

c) $\sqrt{16x^2}=|-20|$.

Lời giải:

a) $\sqrt{x^2}=15$

$\iff$ |x| = 15

$\iff$ x = ± 15.

Vậy x = ± 15.

b) $\sqrt{9x^2}=12$

$\iff \sqrt{{\left(3x\right)}^2}=12$

$\iff$ |3x| = 12

$\iff$ 3x = ± 12

$\iff$ x = ± 4.

Vậy x = ± 4.

d) $\sqrt{16x^2}=|-20|$

$\iff \sqrt{{\left(4x\right)}^2}=20$

$\iff$ |4x| = 20

$\iff$ 4x = ± 20

$\iff$ x = ± 5.

Vậy x = ± 5

Bài 7. Áp dụng quy tắc khai phương một tích, hãy tính:

a) $\sqrt{\mathrm{0,49}.36}$;

b) $\sqrt{\mathrm{14,4}.640}$;

c) $\sqrt{3^4.5^2}$.

Lời giải:

a)

$$\begin{gathered} \sqrt{\mathrm{0,49}.36}=\sqrt{\mathrm{0,49}}.\sqrt{36} \\ =\mathrm{0,7}.6=\mathrm{4,2} \end{gathered}$$

b)

$$\begin{gathered} \sqrt{\mathrm{14,4}.640}=\sqrt{144.64} \\ =\sqrt{144}.\sqrt{64} \end{gathered}$$

= 12 . 8 = 96.

c)

$$\begin{gathered} \sqrt{3^4.5^2}=\sqrt{3^4}.\sqrt{5^2} \\ =3^2.5=45 \end{gathered}$$

Bài 8. Áp dụng quy tắc nhân các căn bậc hai, hãy tính:

a) $\sqrt{8}.\sqrt{32}$;

b) $\sqrt{\mathrm{0,4}}.\sqrt{\mathrm{8,1}}$;

c) $\sqrt{\mathrm{0,03}}.\sqrt{5}.\sqrt{15}$. 

Lời giải:

a)

$$\begin{gathered} \sqrt{8}.\sqrt{32}=\sqrt{8.32} \\ =\sqrt{8.2.16} \end{gathered}$$

$=\sqrt{16.16}=\sqrt{{\left(16\right)}^2}=16$

b)

$$\begin{gathered} \sqrt{\mathrm{0,4}}.\sqrt{\mathrm{8,1}}=\sqrt{\mathrm{0,4}.\mathrm{8,1}} \\ =\sqrt{4.81} \end{gathered}$$

$=\sqrt{{(2.9)}^2}=2.9=18$

c)

$$\begin{gathered} \sqrt{\mathrm{0,03}}.\sqrt{5}.\sqrt{15} \\ =\sqrt{\mathrm{0,03}.5.15} \end{gathered}$$

$$\begin{gathered} =\sqrt{(\mathrm{0,3}.5).\left(\mathrm{0,1.}15\right)} \\ =\sqrt{\mathrm{1,5}.\mathrm{1,5}}=\sqrt{{\left(\mathrm{1,5}\right)}^2}=\mathrm{1,5} \end{gathered}$$

Bài 9. Rút gọn các biểu thức sau:

a) $\sqrt{\mathrm{0,64}{a}^2}$ với a < 0;

b) $\sqrt{a^4{(a-5)}^2}$ với a ≥ 5;

c) $\sqrt{\frac{a}{5}}.\sqrt{\frac{5a}{9}}$ với a ≥ 0.

Lời giải:

a) Vì a < 0 nên |a| = − a.

Ta có: $\sqrt{\mathrm{0,64}{a}^2}=\sqrt{\mathrm{0,64}}.\sqrt{a^2}$ = 0,8 |a|

= 0,8. (− a) = − 0,8a.

b) Vì a² ≥ 0 nên | a² | = a².

Vì a ≥ 5 nên a – 5 ≥ 0.

Suy ra |a – 5| = a – 5.

Ta có: $\sqrt{a^4{(a-5)}^2}=\sqrt{a^4}.\sqrt{{(a-5)}^2}$

= a² . |a – 5| = a² . (a – 5) = a³ – 5a².

c) Ta có:

$$\begin{gathered} \sqrt{\frac{a}{5}}.\sqrt{\frac{5a}{9}}=\sqrt{\frac{a}{5}.\frac{5a}{9}} \\ =\sqrt{\frac{a.5a}{5.9}} \end{gathered}$$

$$\begin{gathered} =\sqrt{\frac{a^2}{9}}=\sqrt{\frac{a^2}{3^2}}=\sqrt{{\left(\frac{a}{3}\right)}^2} \\ =\left|\frac{a}{3}\right|=\frac{a}{3} \end{gathered}$$

(Vì a ≥ 0 nên $\frac{a}{3}\ge 0$, do đó $\left|\frac{a}{3}\right|=\frac{a}{3}$).

Bài 10. Tính:

a) $\sqrt{\frac{121}{256}}$;

b) $\sqrt{1\frac{15}{49}}$;

c) $\sqrt{\frac{\mathrm{4,9}}{\mathrm{16,9}}}$.

Lời giải:

a) $\sqrt{\frac{121}{256}}=\frac{\sqrt{121}}{\sqrt{256}}=\frac{11}{16}$.

b)

$$\begin{gathered} \sqrt{1\frac{15}{49}}=\sqrt{\frac{64}{49}} \\ =\frac{\sqrt{64}}{\sqrt{49}}=\frac{8}{7} \end{gathered}$$

c)

$$\begin{gathered} \sqrt{\frac{\mathrm{4,9}}{\mathrm{16,9}}}=\sqrt{\frac{49}{169}} \\ =\frac{\sqrt{49}}{\sqrt{169}}=\frac{7}{13} \end{gathered}$$

Bài 11. Tính:

a) $\frac{\sqrt{3}}{\sqrt{48}}$;

b) $\frac{\sqrt{245}}{\sqrt{5}}$;

c) $\frac{\sqrt{{24}^7}}{\sqrt{3^5.8^7}}$.

Lời giải:

a) $\frac{\sqrt{3}}{\sqrt{48}}=\sqrt{\frac{3}{48}}=\sqrt{\frac{1}{16}}=\frac{1}{4}$.

b) $\frac{\sqrt{245}}{\sqrt{5}}=\sqrt{\frac{245}{5}}=\sqrt{49}=7$ .

c)

$$\begin{gathered} \frac{\sqrt{{24}^7}}{\sqrt{3^5.8^7}}=\sqrt{\frac{{24}^7}{3^5.8^7}} \\ =\sqrt{\frac{3^7.8^7}{3^5.8^7}} \end{gathered}$$

$=\sqrt{\frac{3^7}{3^5}}=\sqrt{3^2}=3$

Bài 12. Rút gọn biểu thức:

a) $\frac{x}{y}.\sqrt{\frac{9x^2}{y^4}}$ với x < 0, y ≠ 0;

b) $3xy.\sqrt{\frac{36x^4}{y^2}}$ với y > 0;

c) $2x{y}^3.\sqrt{\frac{64}{x^2{y}^4}}$ với x > 0, y ≠ 0.

Lời giải:

a) Ta có: $\frac{x}{y}.\sqrt{\frac{9x^2}{y^4}}=\frac{x}{y}.\frac{\sqrt{9x^2}}{\sqrt{y^4}}$

$$\begin{gathered} =\frac{x}{y}.\frac{\sqrt{9}.\sqrt{x^2}}{\sqrt{{\left(y^2\right)}^2}} \\ =\frac{x}{y}.\frac{3\left|x\right|}{\left|y^2\right|} \end{gathered}$$

Vì x < 0 nên |x| = − x.

Vì y ≠ 0 nên y² > 0. Suy ra | y² | = y².

Do đó

$$\begin{gathered} \frac{x}{y}.\frac{3\left|x\right|}{\left|y^2\right|} \\ =\frac{x}{y}.\frac{3.(-x)}{y^2} \\ =\frac{-3x^2}{y^3} \end{gathered}$$

Vậy $\frac{x}{y}.\sqrt{\frac{9x^2}{y^4}}=\frac{-3x^2}{y^3}$ với x < 0, y ≠ 0.

b)

$$\begin{gathered} 3xy.\sqrt{\frac{36x^4}{y^2}} \\ =3xy.\frac{\sqrt{36x^4}}{\sqrt{y^2}} \\ =3xy.\frac{\sqrt{6^2.{\left(x^2\right)}^2}}{\sqrt{y^2}} \end{gathered}$$

$$\begin{gathered} =3xy.\frac{\sqrt{{\left(6x^2\right)}^2}}{\sqrt{y^2}} \\ =3xy.\frac{\left|6x^2\right|}{\left|y\right|} \end{gathered}$$

Vì x² ≥ 0 nên | x² | = x².

Vì y > 0 nên |y| = y.

Do đó

$$\begin{gathered} 3xy.\frac{\left|6x^2\right|}{\left|y\right|} \\ =3xy.\frac{6x^2}{y}=18x^3 \end{gathered}$$

Vậy $3xy.\sqrt{\frac{36x^4}{y^2}}=18x^3$ với y > 0.

c)  

$2x{y}^3.\sqrt{\frac{64}{x^2{y}^4}}=2x{y}^3.\frac{\sqrt{64}}{\sqrt{x^2{y}^4}}$

$$\begin{gathered} =2x{y}^3.\frac{\sqrt{8^2}}{\sqrt{x^2}.\sqrt{{\left(y^2\right)}^2}} \\ =2x{y}^3.\frac{8}{\left|x\right|.\left|y^2\right|} \end{gathered}$$

Vì x > 0 nên |x| = x.

Vì y ≠ 0 nên y² > 0. Suy ra | y² | = y².

Do đó

$$\begin{gathered} 2x{y}^3.\frac{8}{\left|x\right|.\left|y^2\right|} \\ =2x{y}^3.\frac{8}{x{y}^2}=16y \end{gathered}$$

Vậy $2x{y}^3.\sqrt{\frac{64}{x^2{y}^4}}=16y$ với x > 0, y ≠ 0.

Bài 13. Dùng bảng số để tìm căn bậc hai số học của 115 và 9691 rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả.

Lời giải:

* Căn bậc hai của 115:

- Dùng bảng căn bậc hai:

Ta có:

$$\begin{gathered} \sqrt{115}=\sqrt{100}.\sqrt{\mathrm{1,15}} \\ =10.\sqrt{\mathrm{1,15}} \end{gathered}$$

Tại hàng 1,5 cột 5:

$$\begin{gathered} 10.\sqrt{\mathrm{1,15}}\approx 10.\mathrm{1,072} \\ =\mathrm{10,72} \end{gathered}$$

- Dùng máy tính: $\sqrt{115}\approx \mathrm{10,72380529}$.

Ta thấy sử dụng máy tính cho kết quả chính xác hơn.

* Căn bậc hai của 9691:

- Dùng bảng căn bậc hai:

Ta có:

$$\begin{gathered} \sqrt{9691}=\sqrt{100}.\sqrt{\mathrm{96,91}} \\ =10.\sqrt{\mathrm{96,91}} \end{gathered}$$

+ Tại hàng 96 cột 9: $\sqrt{\mathrm{96,91}}\approx \mathrm{9,844}$.

+ Tại giao của hàng 96 và cột 1 hiệu chính ta thấy số 0.

Nên $\sqrt{\mathrm{96,91}}\approx \mathrm{9,844}$ suy ra $\sqrt{9691}=10.\mathrm{9,844}=\mathrm{98,44}$.

- Dùng máy tính: $\sqrt{115}\approx \mathrm{98,44287684}$.

Ta thấy sử dụng máy tính cho kết quả chính xác hơn.

Bài 14. Biết $\sqrt{\mathrm{9,119}}\approx \mathrm{3,019}$ . Hãy tính:

$\sqrt{91190}$; $\sqrt{\mathrm{0,09119}}$.

Lời giải:

$$\begin{gathered} \sqrt{91190}=\sqrt{9119.10000} \\ =\sqrt{91190}.\sqrt{10000} \end{gathered}$$

≈ 3,019 . 100 = 301,9;

 $$\begin{gathered} \sqrt{\mathrm{0,09119}}=\sqrt{9119:100} \\ =\sqrt{9119}:\sqrt{100} \end{gathered}$$

≈ 3,019 : 10 = 0,3019.

Bài 15. So sánh:

a) $5\sqrt{2}$ và $\sqrt{38}$;

b) $4\sqrt{3}$ và 8.

Lời giải:

a) Ta có:

$$\begin{gathered} 5\sqrt{2}=\sqrt{5^2.2} \\ =\sqrt{25.2}=\sqrt{50} \end{gathered}$$

Vì 50 > 38 nên $\sqrt{50}>\sqrt{38}$ hay $5\sqrt{2}>\sqrt{38}$.

Vậy $5\sqrt{2}>\sqrt{38}$.

b) Ta có:

$$\begin{gathered} 4\sqrt{3}=\sqrt{4^2.3} \\ =\sqrt{16.3}=\sqrt{48} \end{gathered}$$

$8=\sqrt{8^2}=\sqrt{64}$.

Vì 48 < 64 nên $\sqrt{48}<\sqrt{64}$ hay $4\sqrt{3}<8$.

Vậy $4\sqrt{3}<8$.

Bài 16. Rút gọn

a) $\frac{5}{x^2-y^2}\sqrt{\frac{2{(x+y)}^2}{5}}$ với x ≥ 0, y ≥ 0 và x ≠ y;

b) $\frac{3}{a-2}\sqrt{6a^2(a^2-4a+4)}$ với a > 2.

Lời giải:

a) Vì x ≥ 0 và y ≥ 0 nên x + y ≥ 0.

Khi đó, |x + y| = x + y.

Ta có:

$$\begin{gathered} \frac{5}{x^2-y^2}\sqrt{\frac{2{(x+y)}^2}{5}} \\ =\frac{5}{x^2-y^2}\sqrt{\frac{2}{5}.{(x+y)}^2} \end{gathered}$$

$$\begin{gathered} =\frac{5}{x^2-y^2}.\sqrt{\frac{2}{5}}.\sqrt{{(x+y)}^2} \\ =\frac{|x+y|}{(x+y)(x-y)}.5.\sqrt{\frac{2}{5}} \end{gathered}$$

$=\frac{(x+y)}{(x+y)(x-y)}.\sqrt{\frac{5^2.3}{5}}$

$=\frac{1}{x-y}.\sqrt{15}=\frac{\sqrt{15}}{x-y}$

b) Ta có: $\frac{3}{a-2}\sqrt{6a^2(a^2-4a+4)}$

$=\frac{3}{a-2}\sqrt{6a^2(a^2-2.2.a+2^2)}$

$=\frac{3}{a-2}\sqrt{6a^2{(a-2)}^2}$

$=\frac{3}{a-2}.\sqrt{6}.\sqrt{a^2}.\sqrt{{(a-2)}^2}$

$=\frac{3}{a-2}.\sqrt{6}.\left|a\right|.|a-2|$

Vì a > 2 nên a > 0 suy ra |a| = a.

Vì a > 2 nên |a – 2| = a – 2.

Do đó,

$$\begin{gathered} \frac{3}{a-2}.\sqrt{6}.\left|a\right|.|a-2| \\ =\frac{3}{a-2}.\sqrt{6}.a.(a-2) \end{gathered}$$

$=3a\sqrt{6}$

Vậy $\frac{3}{a-2}\sqrt{6a^2(a^2-4a+4)}=3a\sqrt{6}$.

Bài 17. Thực hiện phép tính:

a) $(2\sqrt{2}-\sqrt{3})\sqrt{2}+2\sqrt{6}$;

b)

$$\begin{gathered} \frac{1}{3}\sqrt{27}+2\sqrt{75} \\ -\frac{\sqrt{99}}{\sqrt{11}}+3\sqrt{1\frac{1}{3}} \end{gathered}$$ 

Lời giải:

a)

$(2\sqrt{2}-\sqrt{3})\sqrt{2}+2\sqrt{6}$

$=2\sqrt{2}.\sqrt{2}-\sqrt{3}.\sqrt{2}+2\sqrt{6}$

$=4-\sqrt{6}+2\sqrt{6}$

$=4+\sqrt{6}$

b)

$$\begin{gathered} \frac{1}{3}\sqrt{27}+2\sqrt{75} \\ -\frac{\sqrt{99}}{\sqrt{11}}+3\sqrt{1\frac{1}{3}} \end{gathered}$$

$$\begin{gathered} =\frac{1}{3}.3\sqrt{3}+2.5\sqrt{3} \\ -\sqrt{\frac{99}{11}}+3\sqrt{\frac{4}{3}} \end{gathered}$$

$$\begin{gathered} =\sqrt{3}+10\sqrt{3} \\ -\sqrt{9}+3.\frac{2}{\sqrt{3}} \end{gathered}$$

$=11\sqrt{3}-3+2\sqrt{3}$

$=13\sqrt{3}-3$

Bài 18. Rút gọn biểu thức:

$$\begin{gathered} P=\left(\frac{2}{\sqrt{x}-2}+\frac{\sqrt{x}-1}{2\sqrt{x}-x}\right) \\ :\left(\frac{\sqrt{x}+2}{\sqrt{x}}-\frac{\sqrt{x}-1}{\sqrt{x}-2}\right) \end{gathered}$$

Lời giải:

ĐKXĐ: x > 0; x ≠ 4.

$$\begin{gathered} P=\left(\frac{2}{\sqrt{x}-2}+\frac{\sqrt{x}-1}{2\sqrt{x}-x}\right) \\ :\left(\frac{\sqrt{x}+2}{\sqrt{x}}-\frac{\sqrt{x}-1}{\sqrt{x}-2}\right) \end{gathered}$$

$$\begin{gathered} =\left[\frac{2}{\sqrt{x}-2}-\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}\right] \\ :\left(\frac{\sqrt{x}+2}{\sqrt{x}}-\frac{\sqrt{x}-1}{\sqrt{x}-2}\right) \end{gathered}$$

$$\begin{gathered} =\left[\frac{2\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}-\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}\right] \\ :\left[\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}-\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-2)}\right] \end{gathered}$$

$$\begin{gathered} =\frac{2\sqrt{x}-\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-2)} \\ :\left[\frac{x-4}{\sqrt{x}(\sqrt{x}-2)}-\frac{x-\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}\right] \end{gathered}$$

$=\frac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-2)}:\frac{x-4-x+\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}$

$=\frac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-2)}:\frac{\sqrt{x}-4}{\sqrt{x}(\sqrt{x}-2)}$

$=\frac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{\sqrt{x}-4}$

$=\frac{\sqrt{x}+1}{\sqrt{x}-4}$

Bài 19. Rút gọn:

a) $\sqrt[3]{27x^3}-6x$;

b) $\sqrt[3]{{(a-1)}^3}+\sqrt{{(3a-1)}^2}$ với $a\ge \frac{1}{3}$.

Lời giải:

a) 

$$\begin{gathered} \sqrt[3]{27x^3}-6x \\ =\sqrt[3]{27}.\sqrt[3]{x^3}-6x \end{gathered}$$

= 3x – 6x = – 3x.

b) Vì $a\ge \frac{1}{3}$ nên $a-\frac{1}{3}\ge 0$ suy ra |3a – 1| = 3a – 1.

$\sqrt[3]{{(a-1)}^3}+\sqrt{{(3a-1)}^2}$ = a – 1 + |3a – 1|

= a – 1 + 3a – 1 = 4a – 2.

Bài 20. Tính S = x³ + 12x – 8 khi $x=\sqrt[3]{4+\sqrt{80}}-\sqrt[3]{\sqrt{80}-4}$.

Lời giải:

Ta có: $x^3={\left(\sqrt[3]{4+\sqrt{80}}-\sqrt[3]{\sqrt{80}-4}\right)}^3$

$\iff x^3=\left[4+\sqrt{80}-(\sqrt{80}-4)\right]$

$$\begin{gathered} -3\left(\sqrt[3]{4+\sqrt{80}}-\sqrt[3]{\sqrt{80}-4}\right) \\ .\left(\sqrt[3]{4+\sqrt{80}}.\sqrt[3]{\sqrt{80}-4}\right) \end{gathered}$$

$\iff x^3=8-3x.\left(\sqrt[3]{4+\sqrt{80}}.\sqrt[3]{\sqrt{80}-4}\right)$

$\iff$x³ = 8 – 3x . 4

$\iff$x³ + 12x – 8 = 0.

Vậy khi $x=\sqrt[3]{4+\sqrt{80}}-\sqrt[3]{\sqrt{80}-4}$ thì S = x³ + 12x – 8 = 0.