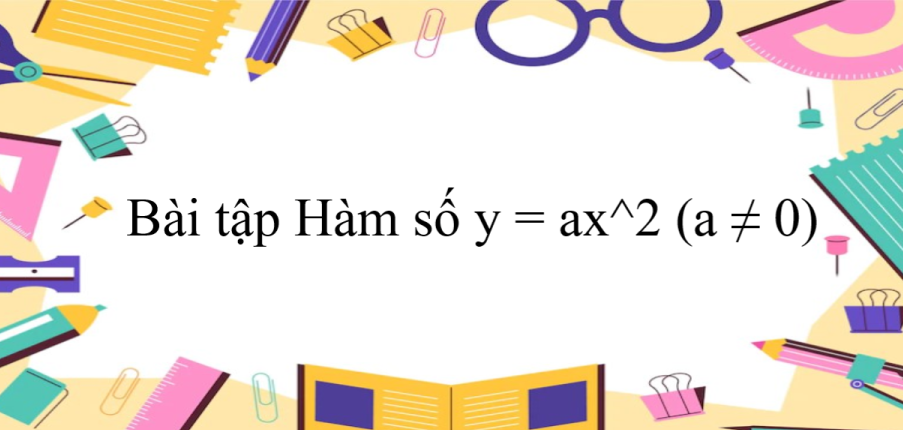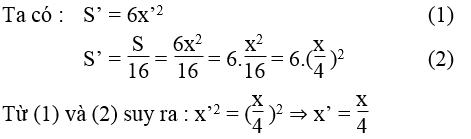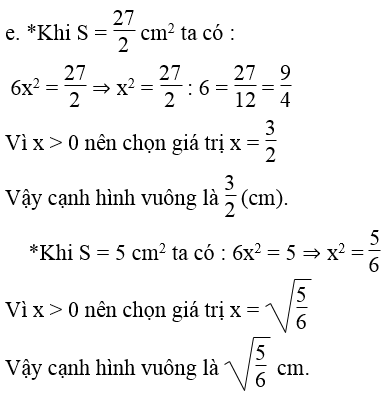Kiến thức cần nhớ
1. Tập xác định
Cho hàm số y=ax2(a≠0)
Tập xác định của hàm số là R.
Ví dụ 1: y=x2; là những hàm số có dạng .
2. Tính chất
Cho hàm số
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Ví dụ 2:
a) Hàm số y = có a = 3 > 0 nên hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
b) Hàm số y = có a = -1 < 0 nên hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
3. Nhận xét
+ Nếu a > 0 thì y > 0 với mọi x ≠ 0; y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số y = 0.
+ Nếu a < 0 thì y < 0 với mọi x ≠ 0; y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0.
Bài tập tự luyện
Bài 1: Diện tích S của hình tròn được tính bởi công thức S = πR2, trong đó R là bán kính của hình tròn.
a) Dùng máy tính bỏ túi, tính các giá trị của S rồi điền vào các ô trống trong bảng sau (π ≈ 3,14, làm tròn kết quả đến chữ số thập phân thứ hai).
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 |
(Xem bài đọc thêm về máy tính bỏ túi dưới đây.)
b) Nếu bán kính tăng gấp 3 lần thì diện tích tăng hay giảm bao nhiêu lần?
c) Tính bán kính của hình tròn, làm tròn kết quả đến chữ số thập phân thứ hai, nếu biết diện tích của nó bằng 79,5 cm2.
Lời giải
a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số:
+ Nhập giá trị:
Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S' = πR'2 = π(3R)2 = π9R2 = 9πR2 = 9S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5
Bài 2: Một vật rơi ở độ cao so với mặt đất là 100m. Quãng đường chuyển động s( mét) của vật rơi phụ thuộc vào thời gian t (giây) bởi công thức: s = 4t2.
a) Sau 1 giây, vật này cách mặt đất bao nhiêu mét? Tương tự, sau 2 giây?
b) Hỏi sau bao lâu vật này tiếp đất?
Lời giải
a) + Sau 1 giây, vật chuyển động được: s(1) = 4.12 = 4m.
Vậy vật cách mặt đất: 100 – 4 = 96 (m).
+ Sau 2 giây, vật chuyển động được: s(2) = 4.22 = 16m
Vậy vật cách mặt đất: 100 – 16 = 84 (m).
b) Vật tiếp đất khi chuyển động được 100m
⇔ 4t2 = 100
⇔ t2 = 25
⇔ t = 5.
Vậy vật tiếp đất sau 5 giây.
Bài 3: Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương vận tốc v của gió, tức là F = av2 (a là hằng số). Biết rằng khi vận tốc gió bằng 2 m/s thì lực tác động lên cánh buồm của một con thuyền bằng 120N (Niu-tơn).
a) Tính hằng số a.
b) Hỏi khi v = 10 m/s thì lực F bằng bao nhiêu? Cùng câu hỏi này khi v =20 m/s?
c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 12000N, hỏi con thuyền có thể đi được trong gió bão với vận tốc gió 90 km/h hay không?
Lời giải
a) Ta có: F = av2
Khi v = 2 m/s thì F = 120N nên ta có: 120 = a.22 ⇔ a = 30.
b) Do a= 30 nên lực F được tính bởi công thức : F = 30v2.
+ Với v = 10m/s thì F(10) = 30.102 = 3000 (N)
+ Với v = 20 m/s thì F(20) = 30.202 = 12000 (N)
c) Ta có 90km/h = 25 m/s.
Với v = 25m/s thì F(25) = 30.252 = 18750 (N) > 12000 (N)
Vậy con thuyền không thể đi được trong gió bão với vận tốc gió 90km/h.
Bài 4: Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
a. Biểu diễn diện tích toàn phần S (tức là tổng diện tích của sáu mặt) của hình lập phương qua x.
b. Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
| x | 1/3 | 1/2 | 1 | 3/2 | 2 | 3 |
| S |
c. Nhận xét sự tăng, giảm của S khi x tăng.
d. Khi S giảm 16 lần thì cạnh x tăng hay giảm bao nhiêu lần ?
e. Tính cạnh của hình lập phương khi S = 27/2 cm2, S = 5cm2.
Lời giải:
a. Diện tích của một mặt hình lập phương là x2.
Hình lập phương có 6 mặt nên có diện tích toàn phần 6x2.
b. Giá trị của S và x được thể hiện trong bảng sau:
| x | 1/3 | 1/2 | 1 | 3/2 | 2 | 3 |
| S | 2/3 | 3/2 | 6 | 27/2 | 24 | 54 |
c. Khi giá trị của x tăng thì giá trị của S tăng.
d. Gọi S’ là giá trị của S khi giảm đi 16 lần, x’ là cạnh hình lập phương khi S giảm đi 16 lần.
Vậy khi S giảm đi 16 lần thì cạnh hình vuông giảm đi 4 lần.
Bài 5: Cho hàm số y = 3x2.
a. Lập bảng tính các giá trị của y ứng với các giá trị của x lần lượt bằng : -2 ; -1 ; -1/3 ; 0 ; 1/3 ; 1 ; 2
b. Trên mặt phẳng tọa độ xác định các điểm mà hoành độ là giá trị của x còn tung độ là giá trị tương ứng của y đã tìm ở câu a.
Chẳng hạn, điểm A(-1/3 ; 1/3 )
Lời giải:
a)
b. Các điểm được thể hiện trên hình vẽ dưới.
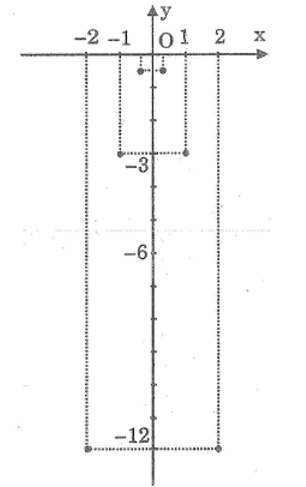
Bài 6: Cho hàm số y = -3x2.
a. Lập bảng các giá trị của y ứng với các giá trị của x lần lượt bằng : -2 ; -1 ; -1/3 ; 0 ; 1/3 ; 1 ; 2
b. Trên mặt phẳng tọa độ xác định các điểm mà hoành độ là giá trị của x còn tung độ là giá trị tương ứng của y đã tìm ở câu a.
Chẳng hạn, điểm A(-1/3 ; -1/3 )
Lời giải:
a)
b) Các điểm được thể hiện trên hình vẽ dưới.
Bài 7: Cho hàm số y = f(x) = -1,5x2
a. Hãy tính f(1), f(2), f(3) rồi sắp xếp các giá trị này theo thứ tự từ lớn đến bé.
b. Hãy tính f(-3), f(-2), f(-1) rồi sắp xếp các giá trị này theo thứ tự từ bé đến lớn.
c. Phát biểu nhận xét của em về sự đồng biến hay nghịch biến của hàm số này khi x > 0 ; khi x < 0
Lời giải:
a. Ta có: f(1) = -1,5.12 = -1,5
f(2) = -1,5.22 = -6
f(3) = -1,5.32 = -13,5
Theo thứ tự từ lớn đến bé : -1,5; -6; -13,5.
b. Ta có: f(-3)= -1,5.(-3)2 = -13,5
f(-2) = -1,5.(-2)2 = -6
f(-1) = -1,5.(-1)2 = -1,5
Theo thứ tự từ bé đến lớn : -13,5 ; -6 ; -1,5.
c. Hàm số y = f(x) = -1,5x2 có hệ số a = -1,5 < 0 nên hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Bài 8: Đố: Một hòn bi lăn trên một mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian bởi công thức y = at2, t tính bằng giây, y tính bằng mét. Kết quả kiểm nghiệm được cho bởi bảng sau:
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 0,24 | 1 | 4 |
a. Biết rằng chỉ có một lần đo không cẩn thận, hãy xác định hệ số a và đố em biết lần nào đo không cẩn thận ?
b. Có một thời điểm dừng hòn bi lại nhưng quên không tính thời gian, tuy nhiên đo được đoạn đường đi được của hòn bi (kể từ thời điểm xuất phát đến điểm dừng) là 6,25m. Đố em biết lần ấy hòn bi đã lăn bao lâu ?
c. Hãy điền tiếp vào các ô trống còn lại ở bảng trên.
Lời giải:
c)
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 0,24 | 1 | 9/4 | 4 | 25/4 | 9 |
Bài 9: Biết rằng nhiệt lượng tỏa ra trên dây dẫn được tính bởi công thức : Q = 0,24RI2t. Trong đó Q là nhiệt lượng tính bằng calo, R là điện trở tính bằng ôm ( Ω), I là cường độ dòng điện tính bằng ampe (A), t là thời gian tính bằng giây (s). Dòng điện chạy qua một dây dẫn có điện trở R = 10 Ω trong thời gian 1 giây.
a. Hãy điền các số thích hợp vào bảng sau :
| I (A) | 1 | 2 | 3 | 4 |
| Q (calo) |
b. Hỏi cường độ dòng điện là bao nhiêu thì nhiệt lượng tỏa ta ra bằng 60 calo ?
Lời giải:
a. Thay R = 10 Ω, t = 1s vào công thức Q = 0,24RI2t, ta có :
Q = 0,24.10.I2.1 = 2,4I2
Giá trị của Q được thể hiện trong bảng sau :
| I (A) | 1 | 2 | 3 | 4 |
| Q (calo) | 2,4 | 9,6 | 21,6 | 38,4 |
b. Nhiệt lượng tỏa ra là 60 calo nghĩa là Q = 60.
Ta có : 60 = 2,4I2 ⇒ I2 = 60/(2,4) = 25
Vậy I = 5 (A).