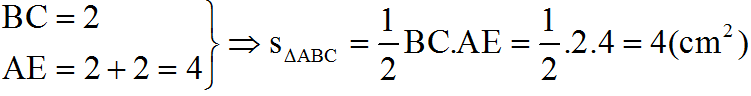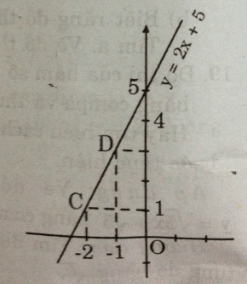50 Bài tập Đồ thị của hàm số y = ax + b (có đáp án năm 2023) - Toán 9

Kiến thức cần nhớ 

1. Đồ thị hàm số y = ax + b (a ≠ 0)

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

- Cắt trục tung tại điểm có tung độ bằng b.

- Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0

Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.

Ví dụ 1. Gọi A là giao điểm của hai đường thẳng y = x − 1 và y = 3x + 1, tìm tọa độ của điểm A?

Lời giải:

Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:

x − 1 = 3x + 1

$\iff$ 3x − x = − 1 − 1

$\iff$ 2x = − 2

$\iff$ x = − 1.

Với x = − 1 thì y = − 1 − 1 = − 2. Khi đó, A(− 1; − 2).

Vậy tọa độ giao điểm A(− 1; − 2).

2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).

• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì $x=\frac{-b}{a}$, ta được điểm $Q\left(-\frac{b}{a};0\right)$ thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).

 Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.

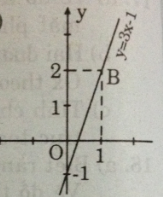
Ví dụ 2. Vẽ đồ thị hàm số y = 2x – 1.

Bước 1: Cho x = 0 thì y = −1, ta được điểm A(0; −1) ∈ Oy.

Cho y = 1 thì 2x – 1 = 1 $\iff$ x = 1, ta được điểm B(1; 1)

Bước 2: Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x – 1.

Ta có đồ thị hàm số:

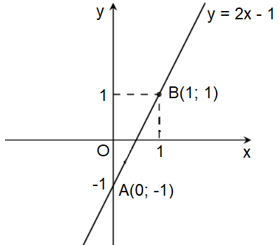
Bài tập tự luyện 

Bài 1: 

a) Vẽ đồ thị của các hàm số

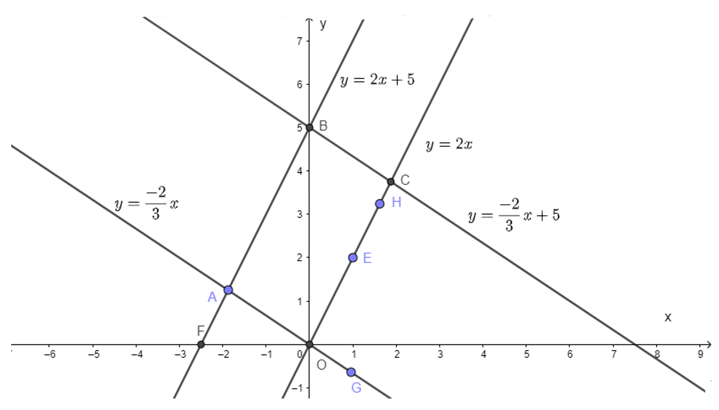
y = 2x; y = 2x + 5; y = $-\frac{2}{3}$x; y  = $-\frac{2}{3}$x + 5 trên cùng một mặt phẳng tọa độ.

b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình bình hành không? Vì sao?

Lời giải:

a)

+ Xét đường thẳng y = 2x

Đường thằng này đi qua góc tọa độ và điểm E (1; 2)

+ Đường thẳng y = 2x + 5 đi qua B (0; 5) và F $\left(\frac{-5}{2}; 0\right)$

+ Đường thẳng y = $-\frac{2}{3}$x đi qua O (0; 0) và điểm G $\left(1; \frac{-2}{3}\right)$

+ Đường thẳng y = $-\frac{2}{3}$x + 5 đi qua B (0; 5) và C $\left(\frac{15}{8};\frac{15}{4}\right)$

b) Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.

Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x và đường thẳng y = $-\frac{2}{3}$x song song với đường thẳng y = $-\frac{2}{3}$x + 5 nên tứ giác OABC là hình bình hành.

Bài 2: 

a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.

b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.

c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)

Lời giải:

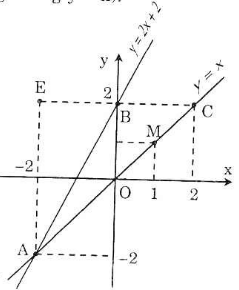
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.

Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.

b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:

        2x + 2 = x

=> x = -2 => y = -2

Suy ra tọa độ giao điểm là A(-2; -2).

c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.

- Tọa độ điểm C:

Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:

    x = 2 => y = 2 => tọa độ C(2; 2)

- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)

Bài 3: 

a) Vẽ đồ thị của các hàm số y = x + 1 và y = -x + 3 trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng y = x + 1 và y = -x + 3 cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C.

c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet)

Lời giải:

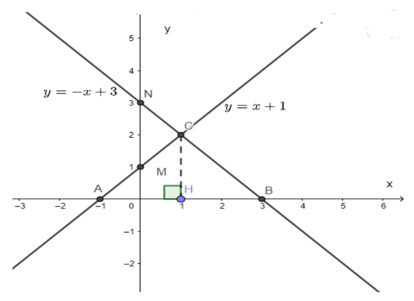
a) - Với hàm số y = x + 1:

Cho x = 0 y = 1 ta được M (0; 1).

Cho y = 0 => x + 1 = 0  x = -1 ta được A (-1; 0).

Nối MA ta được đồ thị hàm số y = x + 1.

- Với hàm số y = -x + 3:

Cho x = 0  y = 3 ta được N (0; 3).

Cho y = 0  -x + 3 = 0  x = 3 ta được B (3; 0).

Nối NB ta được đồ thị hàm số y = -x + 3.

b) Theo câu a ta có đồ thị hàm số y = x + 1 cắt trục Ox tại A (-1; 0)

Theo câu a ta có đồ thị hàm số y = -x + 3 cắt trục Ox tại B (3; 0)

C là giao điểm của hai hàm số nên ta có phương trình hoành độ giao điểm

x + 1 = - x + 3

⇔ x + x = 3 – 1

⇔ 2x = 2

⇔ x = 1y = 2. Vậy C (1; 2)

c) Vì A, B đều năm trên trục hoành, nên nhìn vào đồ thị ta thấy AB = 4cm.

Gọi H là hình chiếu của C lên trục hoành, do đó CH vuông góc với AB, CH là đường cao của tam giác ABC.

Qua đồ thị ta thấy H(1; 2) => CH = 2cm

Diện tích tam giác ABC là:

S_ABC = $\frac{1}{2}$AB.CH = $\frac{1}{2}$.2.4 = 4cm².

Vì A, và H đều nằm trên trục hoành nên qua đồ thị ta thấy AH = 2cm

Vì CHA là tam giác vuông tại H nên ta có:

AC² = AH² + CH² (định lý Py – ta – go)

⇔ AC² = 2² + 2² = 8

=> AC = $\sqrt{8}$cm

Tương tự ta tính được CB = $\sqrt{8}$cm

Chu vi tam giác ABC là

C = AB + BC + CA = 4 + $\sqrt{8}$ + $\sqrt{8}$ = 4 + $2\sqrt{8}$ (cm).

Bài 4: 

a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị B vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1; 3). Tìm a. Vẽ đồ thị hàm số với giá trị a tìm được

Lời giải:

a) Thay x = 4 và y = 11 vào y = 3x + b ta được:

    11 = 3.4 + b = 12 + b

=> b = 11 – 12 = -1

Ta được hàm số y = 3x – 1

- Cho x = 0 => y = -1 được A(0; -1)

- Cho x = 1 => y = 2 được B(1; 2).

Nối A, B ta được đồ thị hàm số y = 3x – 1.

b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:

    3 = a(-1) + 5

=> a = 5 – 3 = 2

Ta được hàm số y = 2x + 5.

- Cho x = -2 => y = 1 được C(-2; 1)

- Cho x = -1 => y = 3 được D(-1; 3)

Nối C, D ta được đồ thị hàm số y = 2x + 5.

Bài 5: Đồ thị của hàm số y = $\sqrt{3}x+\sqrt{3}$ được vẽ bằng compa và thước thẳng (h.8).

Hãy thực hiện cách vẽ đó rồi nêu lại cách thực hiện.

Áp dụng: Vẽ đồ thị của hàm số y = $\sqrt{5}x+\sqrt{5}$ bằng compa và thước thẳng.

Hướng dẫn: Tìm điểm trên trục tung có tung độ bằng $\sqrt{5}$.

Lời giải:

a) Cho x = 0 ⇒ y = $\sqrt{3}$ ta được (0; $\sqrt{3}$).

Cho y = 0 ⇒ $\sqrt{3}x+\sqrt{3}$ = 0 ⇒ x = -1 ta được (-1; 0).

Như vậy để vẽ được đồ thị hàm số y = $\sqrt{3}x+\sqrt{3}$ ta phải xác định được điểm $\sqrt{3}$ trên Oy.

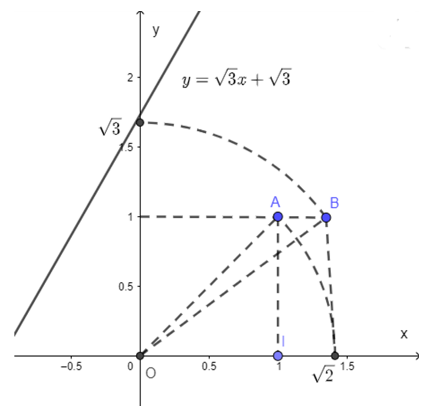
Các bước vẽ đồ thị y = $\sqrt{3}x+\sqrt{3}$

+ Dựng điểm A (1; 1) được OA = $\sqrt{2}$

+ Dựng điểm biểu diễn $\sqrt{2}$ trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn $\sqrt{2}$.

+ Dựng điểm B($\sqrt{2}$; 1) được OB = $\sqrt{3}$

+ Dựng điểm biểu diễn $\sqrt{2}$. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn $\sqrt{3}$

+ Vẽ đường thẳng qua điểm biểu diễn $\sqrt{3}$ trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = $\sqrt{3}x+\sqrt{3}$.

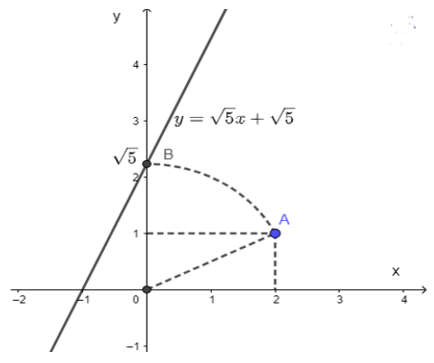
b) Áp dụng vẽ đồ thị hàm số y = $\sqrt{5}x+\sqrt{5}$

- Cho x = 0 ⇒ y = $\sqrt{5}$ ta được (0; $\sqrt{5}$).

- Cho y = 0 ⇒ $\sqrt{5}x+\sqrt{5}$ = 0 ⇒ x = -1 ta được (-1; 0).

Ta phải tìm điểm trên trục tung có tung độ bằng $\sqrt{5}$

Cách vẽ:

+ Dựng điểm A (2; 1) ta được OA = $\sqrt{5}$.

+ Dựng điểm biểu diễn $\sqrt{5}$ trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn $\sqrt{5}$. Vẽ đường thẳng qua điểm biểu diễn $\sqrt{5}$ trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = $\sqrt{5}x+\sqrt{5}$