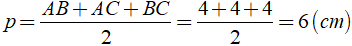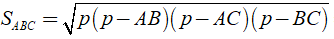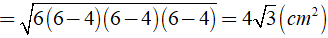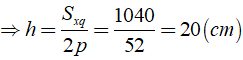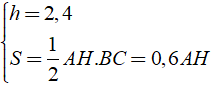30 Bài tập về hình lăng trụ đứng (2024) có đáp án

30 Bài tập về hình lăng trụ đứng

I. Phương pháp giải

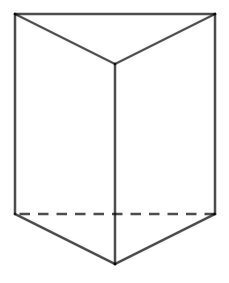
1. Hình lăng trụ đứng

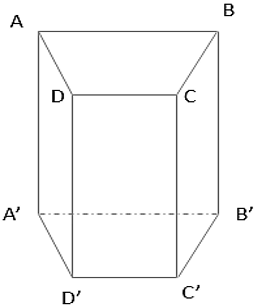
Hình vẽ dưới đây gọi là lăng trụ đứng.

Trong hình lăng trụ đứng này:

+ A, B, C, D, A', B', C', D' là các đỉnh.

+ ABB'A', BCC'B',... là những hình chữ nhật, gọi là các mặt bên

+ AA'; BB'; CC'; DD' song song với nhau và bằng nhau, chúng được gọi là các cạnh bên

+ Hai mặt ABCD và A'B'C'D' là hai đáy. Hình lăng trụ trên có hai đáy là tứ giác nên gọi là lặng trụ tứ giác, kí hiệu : ABCD.A'B'C'D'

Chú ý:

– Hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.

– Các cạnh bên song song, bằng nhau và vuông góc với hai mặt phẳng đáy. Độ dài cạnh bên được gọi chiều cao của hình lăng trụ đứng.

– Các mặt bên là những hình chữ nhật và vuông góc với hai mặt phẳng đáy.

– Hình hộp chữ nhật, hình lập phương là những hình lăng trụ đứng.

– Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.

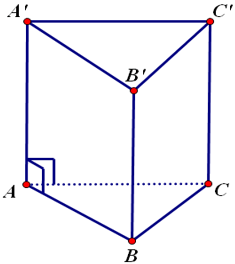
Ví dụ: Cho hình lưng trụ đứng sau:

Hai mặt đáy ABC và A'B'C' là hai tam giác bằng nhau (nằm trong hai mặt phẳng song song)

Các mặt bên A'C'CA, A'B'BA, B'C'CB là các hình chữ nhật.

2. Diện tích – Thể tích của hình lăng trụ đứng

a) Công thức diện tích xung quanh

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao:

S_xq = 2p.h    (p: nửa chu vi đáy, h: chiều cao)

b) Diện tích toàn phần

Diện tích toàn phần của hình lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.

S_tp = S_xq + 2S    (S: điện tích đáy)

c) Thể tích

Thể tích của hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao:

V = S.h    (S: diện tích đáy, h: chiều cao)

d) Ví dụ

Ví dụ: Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều, AB = 4cm,AA' = 5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lặng trụ ABC.A'B'C' ?

Lời giải:

Xét tam giác ABC có nửa chu vi của tam giác là:

Khi đó ta có

+ Diện tích xung quanh của hình lăng trụ S_xq = 2p.AA' = 2.6.5 = 60( cm² )

+ Diện tích toàn phần của hình lăng trụ là S_tp = S_xq + 2S_ABC = 60 + 2.4√ 3 = 60 + 8√ 3 ( cm² )

+ Thể tích của hình lăng trụ là V = S.AA' = 4√ 3 .5 = 20√ 3 ( cm^3 ).

II. Bài tập vận dụng

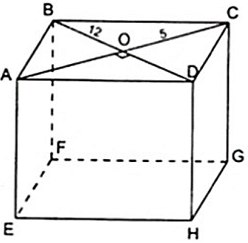
Bài 1: Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm²

Lời giải:

Áp dụng công thức: S_tp = S_xq + 2S_d

Hay S_xq = S_tp - 2S_d = 1280 - 2.1/2.1024

= 1280 - 240 = 1040( cm² )

Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)

Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:

BC² = BO² + OC² ⇒ BC² = 12² + 5² = 13² ⇔ BC = 13( cm )

Chu vi đáy là 2p = 4.13 = 52( cm )

Áp dụng công thức S_xq = 2p.h

Bài 2: Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm³ ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?

Lời giải:

Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h

Ta có:

Do đó: V = S.h = 0,6AH.2,4 = 1,44AH

Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

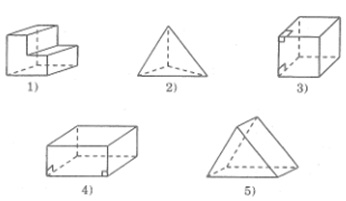
Bài 3: Trong các hình vẽ sau đây, hình vẽ nào biểu diễn một hình lăng trụ đứng?

Lời giải:

Hình số (3), (4), (5) là hình lăng trụ đứng.

Bài 4: Một lăng trụ đứng, đáy là một tam giác thì lăng trụ đó có:

A. 6 mặt, 9 cạnh, 5 đỉnh

B. 5 mặt, 9 cạnh, 6 đỉnh

C. 6 mặt, 5 cạnh, 9 đỉnh

D. 5 mặt, 6 cạnh, 9 đỉnh

Kết quả nào trên đây là đúng?

Lời giải:

Một lăng trụ đứng, đáy là một tam giác thì lăng trụ đó có 5 mặt, 9 cạnh, 6 đỉnh.

Vậy chọn đáp án B

Bài 5: Hãy cho bịết:

a. Một lăng trụ đứng có 6 mặt thì đáy của hình lăng trụ là hình gì?

b. Một lăng trụ đứng có 8 mặt thì đáy của hình lăng trụ là hình gì?

Lời giải:

a. Một lăng trụ đứng có 6 mặt thì đáy là một tứ giác

b, Một lăng trụ đứng có 8 mặt thì đáy của lăng trụ đó là một lục giác

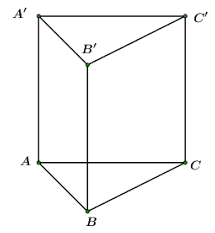
Bài 6: Hình vẽ biểu diễn một lăng trụ đứng có đáy là tam giác. Trong các phát biểu sau, phát biểu nào là đúng?

a) Các cạnh bên AB và AD vuông góc với nhau;

b) Các cạnh bên BE và EF vuông góc với nhau;

c) Các cạnh bên AC và DF vuông góc với nhau

d) Các cạnh bên AC và DF song song với nhau;

e) Hai mặt phẳng (ABC) và (DEF) song song với nhau;

g) Hai mặt phẳng (ACFD) và (BCFE) song song với nhau;

h) Hai mặt phẳng (ABED) và (DEF) vuông góc với nhau.

Lời giải:

a) Sai vì AB không phải là cạnh bên.

b) Sai vì EF không phải là cạnh bên.

c) Sai vì AC và DF không phải là cạnh bên và không vuông góc.

d) Sai vì AC và DF không phải là cạnh bên.

e) Đúng vì mp (ABC) // mp (DEF).

f) Sai vì mp (ACFD) và mp (BCFE) cắt nhau tại FC.

g) Đúng vì mp (ABED) và mp (DEF) vuông góc với nhau.

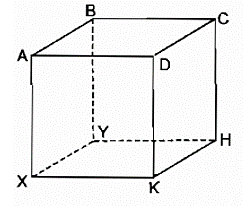
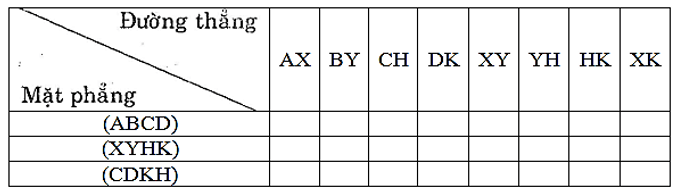
Bài 7: ABCD.XYHK là một lăng trụ đứng có đáy là một hình chữ nhật.

a) Quan sát hình và chỉ ra những cặp mặt phẳng song song với nhau.

b) Những cặp mặt phẳng nào vuông góc với nhau?

c) Hai mặt phẳng (BCHY) và (KXYH) có vuông góc với nhau hay không?

d) Sử dụng kí hiệu // và ⊥ để điền vào các ô trống ở bảng sau:

Lời giải:

a) Những cặp mặt phẳng song song với nhau là:

mp(ABCD) và mp(XYHK)

mp(ADKX) và mp(BCHY)

mp(ABYX) và mp(CDKH)

b) Những cặp mặt phẳng vuông góc với nhau là:

mp (ABCD) và mp(ADKX); mp (XYHK) và mp (ADKX)

mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)

mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)

mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)

mp(ADKX) và mp(CDKH) ;mp (ADKX) và mp (ABYX)

mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)

c) Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau

d) Ta điền như sau:

Chú ý: Những đường thẳng nằm trong mặt phẳng thì không thể song song hoặc vuông góc với mặt phẳng đó.

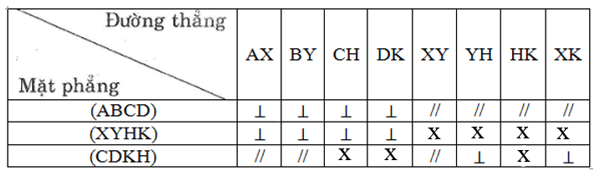
Bài 8: Quan sát các hình khai triển trên hình vẽ dưới rồi cho biết: Cạnh nào sẽ được ghép với cạnh AB để được hình lăng trụ đứng (sử dụng các số cho trên hình)

Lời giải:

Hình a có 5 mặt ghép thành lăng trụ đứng có đáy là tam giác thì cạnh 2 sẽ được ghép với cạnh AB ta sẽ được lăng trụ đứng

Hình b có 5 mặt ghép thành lăng trụ đứng là tam giác có cạnh là AB nên cạnh số 1 ghép với cạnh AB ta sẽ được lăng trụ đứng

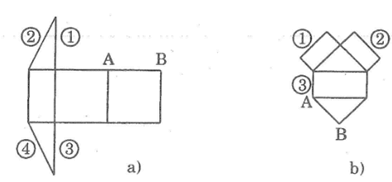
Bài 9: Quan sát hình lăng trụ đứng tam giác ABC.A’B’C’ và hình khai triển của nó. Hãy chỉ ra sự tương ứng giữa các mặt bên với các hình chữ nhật của hình khai triển.

Lời giải:

Hình (1) là hình chữ nhật có độ dài 2 cạnh lần lượt là a và h nên hình (1) là mặt AA’C’C.

Hình (2) là hình chữ nhật có độ dài 2 cạnh lần lượt là b và h nên hình (2) là mặt BB’C’C.

Hình (3) là hình chữ nhật có độ dài 2 cạnh lần lượt là c và h nên hình (3) là mặt AA’B’B.

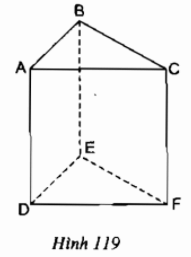
Bài 10: Quan sát lăng trụ đứng tam giác ABC.A'B'C' ở Hình 23 và cho biết: 

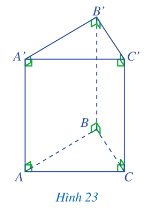a) Đáy dưới ABC và đáy trên A'B'C' là hình gì?

b) Mặt bên AA'C'C là hình gì?

c) So sánh độ dài hai cạnh bên AA' và CC'.

Lời giải:

Ở hình 23 ta quan sát được

a) Đáy dưới ABC và đáy trên A’B’C’ là hình tam giác.

b) Mặt bên AA’C’C là hình gì hình chữ nhật.

c) Độ dài cạnh bên AA’ và CC’ là bằng nhau.

Bài 11: Quan sát lăng trụ đứng tam giác ABCD. A’B’C’D’ ở Hình 27 và cho biết:  

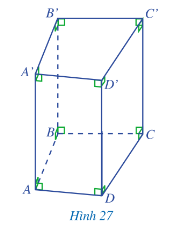a) Đáy dưới ABCD và đáy trên A'B'C'D' là hình gì?

b) Mặt bên AA'D'D là hình gì?

c) So sánh độ dài hai cạnh bên AA' và DD'.

Lời giải:

a) Ta quan sát thấy đáy dưới ABCD và đáy trên A’B’C’D’ là hình tứ giác.

b) Ta quan sát thấy mặt bên AA’D’D là hình hình chữ nhật.

c) Ta quan sát thấy độ dài hai cạnh bên AA’ và DD’ là hai cạnh bằng nhau.

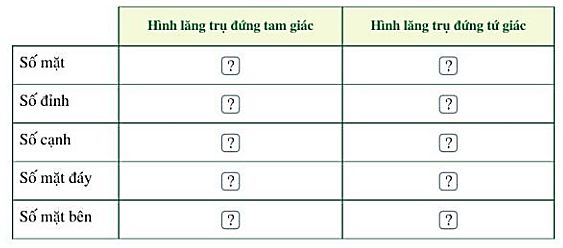
Bài 12: Tìm số thích hợp cho $\boxed{?}$ trong bảng sau: 

Lời giải:

Hình lăng trụ đứng tam giác

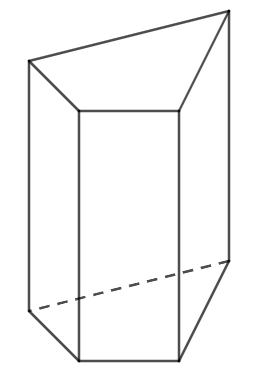
Hình lăng trụ đứng tứ giác

Hình lăng trụ đứng tam giác có 5 mặt; 6 đỉnh; 9 cạnh; 2 mặt đáy; 3 mặt bên.

Hình lăng trụ đứng tam giác có 6 mặt; 8 đỉnh; 12 cạnh; 2 mặt đáy; 4 mặt bên.

Ta có bảng sau: