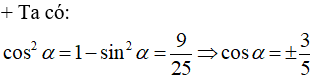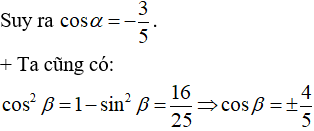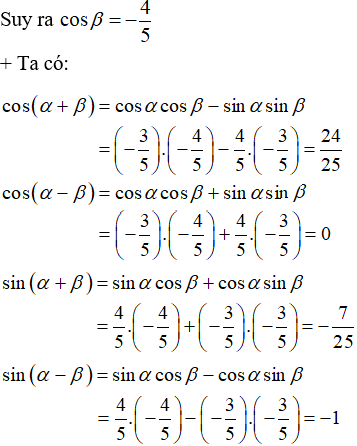Đường tròn lượng giác
Lý thuyết
1. Khái niệm
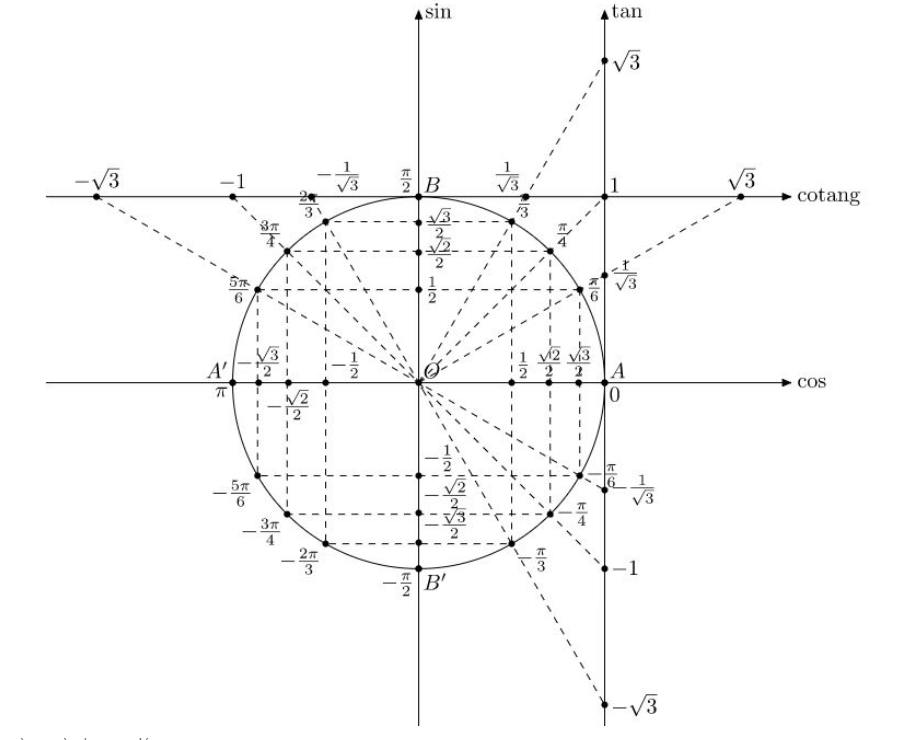
- Vòng tròn lượng giác là đường tròn đơn vị tâm O bán kính 1, định hướng với quy ước chiều dương là chiều ngược chiều kim đồng hồ và trên đó A là điểm gốc.
- Điểm trên đường tròn lượng giác sao cho một điểm C bất kì nằm trên đường tròn ta đều có
được gọi là điểm trên đường tròn lượng giác biểu diễn cung lượng giác có số đo
.
- Trục Ox được gọi là trục giá trị cos.
- Trục Oy được gọi là trục giá trị sin.
- Trục tan có gốc là điểm và vuông góc với trục cos, trục cotan có gốc là điểm vuông góc với trục sin.
2. Dấu của các giá trị lượng giác
Các giá trị của vòng tròn lượng giác sẽ gồm có dấu, bảng giá trị lượng giác từ 0 - 180 độ. Ngoài ra các em cũng cần nắm rõ công thức về các cung liên kết với vòng tròn lượng giác. Cụ thể như sau:
Dấu của giá trị lượng giác
Các giá trị lượng giác trong vòng tròn lượng giác, cũng như các góc ¼ số cụ thể như sau:
-
Giá trị lượng giác Sinx, góc phần tư thứ nhất và góc phần tư thứ 2 mang dấu (+), góc phần tư thứ 3 và góc phần thứ 4 mang dấu (-).
-
Giá trị lượng giác Cosx, góc phần tư thứ nhất và góc phần tư thứ 4 mang dấu (+), góc phần tư thứ 2 và góc phần tư thứ 3 mang dấu (-).
-
Giá trị Tanx, góc phần tư thứ nhất và góc phần tư thứ 3 mang dấu (+), góc phần tư thứ 2 và góc phần tư thứ 4 mang dấu (-).
-
Giá trị Cotx, góc phần thứ nhất nhất và góc phần thứ thứ 3 mang dấu (+), góc phần tư thứ 2 và góc phần tư thứ 4 mang dấu (-).
Để giúp các em dễ dàng ghi nhớ về dấu giá trị lượng giác, dưới đây là bảng tổng hợp ngắn gọn như sau:c
3. Bảng giá trị lượng giác từ 
đến 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
-1 |
0 |
|
|
1 |
|
|
|
0 |
|
|
|
-1 |
0 |
1 |
|
|
0 |
|
1 |
|
|| |
|
-1 |
|
0 |
|| |
0 |
|
|
|| |
|
1 |
|
0 |
|
-1 |
|
|| |
0 |
|| |
4. Công thức các cung liên kết trên đường tròn lượng giác
|
Góc đối nhau ( cos đối) |
Góc bù nhau (sin bù) |
Góc phụ nhau (Phụ chéo) |
Góc hơn kém (Khác pi tan) |
| cos (-α) = cos α | sin (π-α) = sin α | sin (π/2-α)= cos α | sin (π+α) = - sin α |
| sin (-α) = -sin α | cos (π-α) = - cos α | cos (π/2-α) = sinα | cos (π+α) = - cosα |
| tan (-α) = - tan α | tan (π-α) = - tan α | tan (π/2-α) = cot α | tan (π+α) = tanα |
| cot (-α) = -cot α | cot (π-α) = – cot α | cot (π/2-α) = tan α | cot (π+α) = cotα |
Bài tập vận dụng
Bài 1: Cho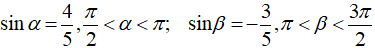 
. Tính cos(α + β), os(α-β), sin(α + β), sin(α - β).
Hướng dẫn giải:
Vì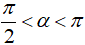 
nên điểm cuối của cung α thuộc góc phần tư thứ II, do đó cosα < 0
Vì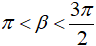 
nên điểm cuối của cung β thuộc góc phần tư thứ III, do đó cosβ < 0
Bài 2: Cho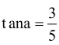 
. Tính:
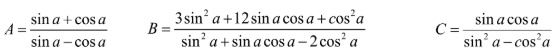
Hướng dẫn giải:
Bài 3: Cho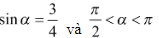 
. Tính:
Hướng dẫn giải:
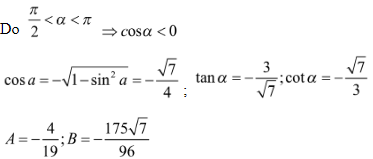
Bài 4: Cho 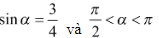. Tính:
Hướng dẫn giải:
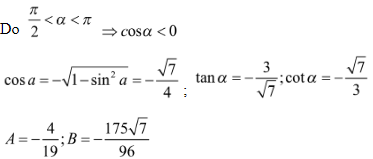
Bài 5: Chứng minh đẳng thức lượng giác:
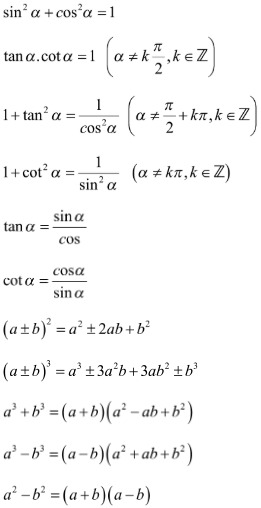
Hướng dẫn giải:
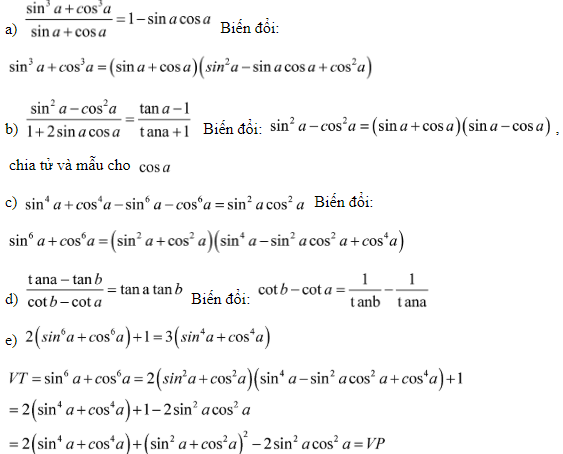
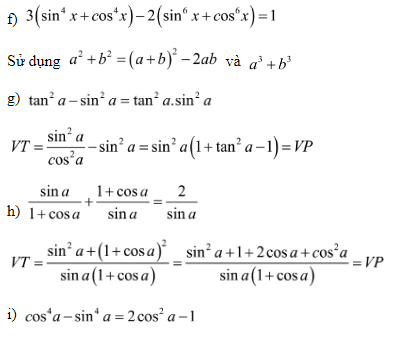
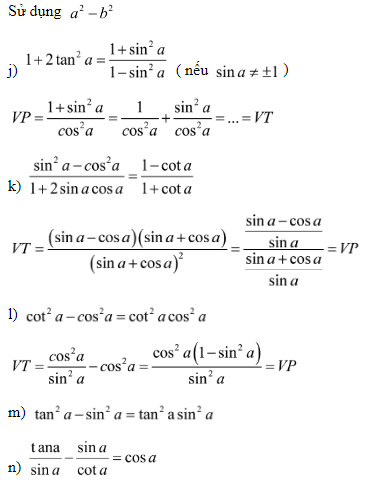
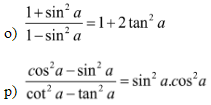
Xem thêm các dạng bài tập Toán liên quan khác:
90 Bài tập giá trị lượng giác của một góc từ 0 độ đến 180 độ (có đáp án năm 2024).
70 Bài tập về một số phương trình lượng giác thường gặp (có đáp án năm 2024)
20 bài tập trắc nghiệm cung lượng giác và góc lượng giác (có đáp án năm 2024).
40 bài tập trắc nghiệm công thức lượng giác (có đáp án năm 2024).
500 Bài tập về hàm số lượng giác và phương trình lượng giác (có đáp án năm 2024).
