20 Bài tập vận tốc trung bình (2024) có đáp án

Bài viết 20 Bài tập vận tốc độ trung bình hay nhất gồm 4 phần: Định nghĩa, Công thức, Kiến thức mở rộng và Bài tập minh họa áp dụng công thức trong bài có lời giải chi tiết giúp học sinh dễ học, dễ nhớ Công thức tính tốc độ trung bình Vật Lí 10.

Bài tập vận tốc trung bình

1. Định nghĩa

- Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng có tốc độ trung bình như nhau trên mọi quãng đường.

- Tốc độ trung bình là đại lượng cho biết mức độ nhanh, chậm của chuyển động và được xác định bằng thương số giữa quãng đường đi được với thời gian chuyển động.

2. Công thức

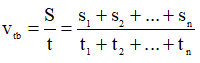
Công thức tính tốc độ trung bình hay nhất

Trong đó:

v_tb: là tốc độ trung bình (m/s)

S: Tổng quãng đường đi được (m)

t: tổng thời gian đi được (s)

s₁, s₂, …s_n là những quãng đường đi được trong những khoảng thời gian t₁, t₂, …, t_n.

3. Kiến thức mở rộng

- Từ công thức tính tốc độ trung bình, ta có thể tính:

+ Thời gian đi được: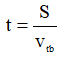

+ Quãng đường đi được: S = v_tb.t

- Bảng đơn vị vận tốc:

Đơn vị đo độ dài	m	m	km	km	cm
Đơn vị đo thời gian	s	phút	h	s	s
Đơn vị đo vận tốc	m/s	m/phút	km/h	km/s	cm/s

- Đơn vị hợp pháp của vận tốc là: m/s và km/h.

Công thức tính tốc độ trung bình hay nhất

Lưu ý:

- Trong chuyển động thẳng khi chiều chuyển động của vật không đổi thì vận tốc trung bình tương đương với tốc độ trung bình vì độ dời trùng với quãng đường đi được.

- Phân biệt giữa quãng đường đi được và độ dời:

+ Quãng đường đi được:

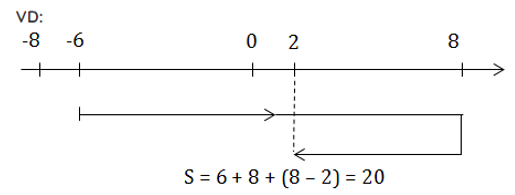
Công thức tính tốc độ trung bình hay nhất

+ Độ dời = độ biến thiên tọa độ = tọa độ cuối - tọa độ đầu

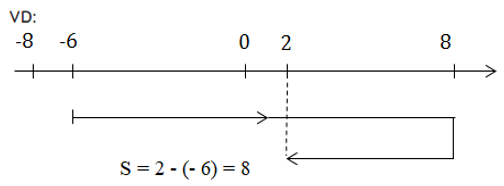
Công thức tính tốc độ trung bình hay nhất

4. Bài tập vận dụng

Bài 1: Cho một xe ô tô chạy trên một quãng đường trong 5h. Biết 2h đầu xe chạy với tốc độ trung bình 60km/h và 3h sau xe chạy với tốc độ trung bình 40km/h.Tính tốc độ trung bình của xe trong suốt thời gian chuyển động.

Lời giải:

S₁ = v₁.t₁ = 120 km

S₂ = v₂.t₂ = 120 km

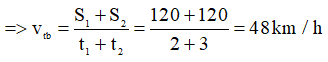
Công thức tính tốc độ trung bình hay nhất

Bài 2: Ô tô chuyển động thẳng từ A đến B. Đầu chặng ô tô đi một phần tư tổng thời gian với v = 50km/h. Giữa chặng ô tô đi một phần hai thời gian với v = 40km/h. Cuối chặng ô tô đi một phần tư tổng thời gian với v = 20km/h. Tính tốc độ trung bình của ô tô?

Lời giải:

Quãng đường đi đầu chặng: 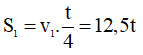Công thức tính tốc độ trung bình hay nhất

Quãng đường chặng giữa: 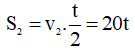Công thức tính tốc độ trung bình hay nhất

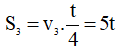
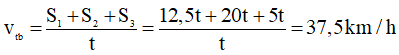
Quãng đường đi chặng cuối: Công thức tính tốc độ trung bình hay nhất

Tốc độ trung bình: Công thức tính tốc độ trung bình hay nhất

Bài 3: Một ô tô chuyển động trên đoạn đường AB. Nửa quãng đường đầu ô tô đi với vận tốc 60 km/h, nửa quãng đường còn lại ô tô đi với nửa thời gian đầu với vận tốc 40 km/h, nửa thời gian sau đi với vận tốc 20 km/h. Xác định vận tốc trung bình cả cả quãng đường AB.

Lời giải:

Giai đoạn 1: 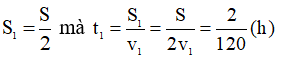Công thức tính vận tốc trung bình hay nhất

Giai đoạn 2: S₂ = v₂.t₂ = 40.t₂

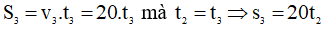
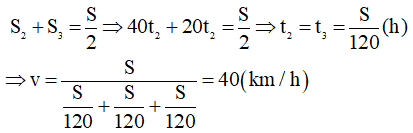
Giai đoạn 3: Công thức tính vận tốc trung bình hay nhất

Công thức tính vận tốc trung bình hay nhất

Bài 4: Một ôtô chuyển động trên đoạn đường MN. Trong một phần hai quãng đường đầu đi với v = 40km/h. Trong một phần hai quãng đường còn lại đi trong một phần hai thời gian đầu với v = 75km/h và trong một phần hai thời gian cuối đi với v = 45km/h. Tính vận tốc trung bình trên đoạn MN.

Lời giải:

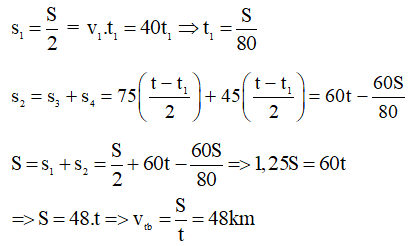
Công thức tính vận tốc trung bình hay nhất

Bài 5: Một người đua xe đạp đi trên 1/3 quãng đường đầu với 25km/h. Tính vận tốc của người đó đi trên đoạn đường còn lại. Biết rằng v_tb = 20km/h.

Hướng dẫn:

$\begin{array}{l} \operatorname{có} S_{1}=v_{1} \cdot t_{1} \Rightarrow t_{1}=\frac{S_{1}}{v_{1}}=\frac{S}{75} \\ S_{2}=v_{2} \cdot t_{2} \Rightarrow t_{2}=\frac{S_{2}}{v_{2}}=\frac{2 S}{3 v_{2}} \\ v_{t b}=\frac{S}{t}=\frac{S}{t_{1}+t_{2}}=20 k m / h \Rightarrow \frac{S}{\frac{S}{75}+\frac{2 S}{3 v_{2}}}=20(k m / h) \\ \Rightarrow 225 v_{2}=60 v_{2}+3000 \Rightarrow v_{2}=18,182(\mathrm{km} / \mathrm{h}) \end{array}$

Bài 6: Một người đi xe máy trên một đoạn đường thẳng AB. Trên một phần ba đoạn đường đầu đi với $v_{1}=30(\mathrm{km} / \mathrm{h})$ , một phần ba đoạn đường tiếp theo với $v_{2}=36(\mathrm{km} / \mathrm{h})$ và một phần ba đoạn đường cuối cùng đi với $v_{3}=48(\mathrm{km} / \mathrm{h})$ . Tính v_tb trên cả đoạn AB.

Hướng dẫn:

Trong một phần ba đoạn đường đầu: $S_{1}=v_{1} \cdot t_{1} \Rightarrow t_{1}=\frac{S_{1}}{v_{1}}=\frac{S}{3 \cdot v_{1}}$

Tương tự: $t_{2}=\frac{S_{2}}{v_{2}}=\frac{S}{3 \cdot v_{2}} ; t_{3}=\frac{S_{3}}{v_{3}}=\frac{S}{3 \cdot v_{3}}$

$v_{t b}=\frac{S}{t_{1}+t_{2}+t_{3}}=\frac{S}{\frac{S}{3 \cdot v_{1}}+\frac{S}{3 \cdot v_{2}}+\frac{S}{3 \cdot v_{3}}}=\frac{1}{\frac{1}{3 \cdot v_{1}}+\frac{1}{3 \cdot v_{2}}+\frac{1}{3 \cdot v_{3}}}=36,62 \mathrm{km} / \mathrm{h}$

Bài 7: Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với $v_{1}=30(\mathrm{km} / \mathrm{h})$ trong 10km đầu tiên; giai đoạn 2 chuyển động với v₂ = 40km/h trong 30 phút; giai đoạn 3 chuyển động trên 4km trong 10 phút. Tính vận tốc trung bình trên cả đoạn đường

Hướng dẫn:

Thời gian xe máy chuyển động giai đoạn đầu $t_{1}=\frac{S_{1}}{v_{1}}=\frac{10}{30}=\frac{1}{3}(h)$

Quãng đường giai đoạn hai chuyển động $S_{2}=v_{2} t_{2}=40 \cdot \frac{1}{2}=20(\mathrm{km})$ $S_{2} = v_{2} t_{2} = 40. \frac{1}{2} = 20 (k m)$

$\begin{array}{l} S=S_{1}+S_{2}+S_{3}=10+20+4=34(k m) \\ t=t_{1}+t_{2}+t_{3}=\frac{1}{3}+\frac{1}{2}+\frac{1}{6}=1 h \\ \Rightarrow v_{t b}=\frac{S}{t}=\frac{34}{1}=34(k m / h) \end{array}$

Bài 8: Một xe máy điện đi nửa đoạn đường đầu tiên với tốc độ trung bình $v_1=24(\mathrm{km}/\mathrm{h})$ và nửa đoạn đường sau với tốc độ trung bình $v_2=40(\mathrm{km}/\mathrm{h})$ . Tính tốc độ trung bình trên cả đoạn đường.

Hướng dẫn:

$t_{1}=\frac{S_{1}}{v_{1}}=\frac{S}{2.24}=\frac{S}{48}$

Thời gian đi nửa đoạn đường cuối: $t_{2}=\frac{S_{2}}{v_{2}}=\frac{S}{2.40}=\frac{S}{80}$

Tốc độ trung bình: $v_{t b}=\frac{S}{t_{1}+t_{2}}=\frac{S}{\frac{S}{48}+\frac{S}{80}}=30(\mathrm{km} / \mathrm{h})$

Bài 9: Một ôtô đi trên quãng đường AB với $v=54(\mathrm{km}/\mathrm{h})$ . Nếu tăng vận tốc thêm $6(\mathrm{km}/\mathrm{h})$ thì ôtô đến B sớm hơn dự định 30 phút. Tính quãng đường AB và thòi gian dự định để đi quãng đường đó.

Hướng dẫn:

$\begin{array}{l} S=v_{1} t=54 t=60(t-0,5) \Rightarrow t=5 h \\ \Rightarrow S=v_{1} t=54.5=270(\mathrm{km}) \end{array}$

Bài 10: Một ôtô đi trên quãng đường AB với $v=72\ (\mathrm{km}/\mathrm{h})$ . Nếu giảm vận tốc đi 18km/h thì ôtô đến B trễ hơn dự định 45 phút. Tính quãng đường AB và thời gian dự tính để đi quãng đường đó.

Hướng dẫn:

$\begin{array}{l} v_{1}=72(k m / h) \Rightarrow v_{2}=72-18=54(k m / h) \\ t_{1} \Rightarrow t_{2}=t_{1}+\frac{3}{4} \\ \text { Mà } S=v_{1} \cdot t_{1}=v_{2} \cdot t_{2} \Rightarrow 72 t_{1}=54\left(t_{1}+\frac{3}{4}\right) \Rightarrow t_{1}=2,25 h \\ S=v_{1} \cdot t_{1}=72.2,25=162(\mathrm{km}) \end{array}$

Bài 11: Một ô tô chuyển động trên đoạn đường AB. Nửa quãng đường đầu ô tô đi với vận tốc 60 km/h, nửa quãng đường còn lại ô tô đi với nửa thời gian đầu với vận tốc 40 km/h, nửa thời gian sau đi với vận tốc 20 km/h. Xác định vận tốc trung bình cả cả quãng đường AB

Hướng dẫn:

$v=\frac{s_{1}+s_{2}+s_{3}}{t_{1}+t_{2}+t_{3}}$

Giai đoạn một: $S_{1}=\frac{S}{2} \text { mà } t_{1}=\frac{S_{1}}{v_{1}}=\frac{S}{2 v_{1}}=\frac{2}{120}(h)$

Giai đoạn 2: $S_{2}=v_{2} \cdot t_{2}=40 . t_{2}$

Giai đoạn 3: $S_{2}+S_{3}=\frac{S}{2} \Rightarrow 40 t_{2}+20 t_{2}=\frac{S}{2} \Rightarrow t_{2}=t_{3}=\frac{S}{120}(h)$

Theo bài ra

$\begin{aligned} &\text S_{2}+S_{3}=\frac{S}{2} \Rightarrow 40 t_{2}+20 t_{2}=\frac{S}{2} \Rightarrow t_{2}=t_{3}=\frac{S}{120}(h)\\ &\Rightarrow v=\frac{S}{\frac{S}{120}+\frac{S}{120}+\frac{S}{120}}=40(k m / h) \end{aligned}$

Bài 12: Lúc 7 giờ một người ở A chuyển động thẳng đều với vận tốc v =50 km/h đuổi theo người B đang chuyển động với vận tốc 30 km/h. Biết khoảng cách AB = 20 km. Viết phương trình chuyển động của hai người. Hỏi hai người đuổi kịp nhau lúc mấy giờ và ở đâu?

Hướng dẫn giải

Chọn gốc tọa độ tại A, gốc thời gian là lúc 7 giờ, chiều dương cùng chiều chuyển động.

Phương trình chuyển động của:

Người A: x_A=x_0A+v_At=0+50t=50t (1)

Người B: x_B=x_0B+v_Bt=20+30t (2)

Khi hai xe gặp nhau:

x_A=x_B⇔50t=20+30t⇔t=1h

Thay t = 1 vào phương trình (1) x_A=50km

Vậy hai xe gặp nhau tại vị trí cách gốc tọa độ 50 km vào lúc 8 giờ.

Bài 13: Hai xe cùng chuyển động đều trên đường thẳng. Nếu chúng đi ngược chiều thì cứ 30 phút khoảng cách của chúng giảm 40km. Nếu chúng đi cùng chiều thì cứ sau 20 phút khoảng cách giữa chúng giảm 8km. Tính vận tốc mỗi xe.

Hướng dẫn:

Chọn chiều dương là chiều chuyển động của mỗi xe.

Nếu đi ngược chiều thì S1 + S2 = 40 ==> $\frac{v_1+v_2}2$ = 40 (1)

Nếu đi cùng chiều thì S1- S2 = (v1 - v2) t = 8 ==> $\frac{v_1-v_2}3$ = 8 (2)

Giải (1) (2): v1 = 52 km/h ; v2 = 28 km/h

Bài 14: Một điểm nằm trên vành ngoài của lốp xe máy cách trục bánh xe 30cm. Bánh xe quay đều với tốc độ 8 vòng/s. Số vòng bánh xe quay để số chỉ trên đồng hồ tốc độ của xe sẽ nhảy 1 số ứng với 1km và thời gian quay hết số vòng ấy là bao nhiêu?

Hướng dẫn:

S = N.2πr = 1000 ⇒ N = 531 vòng

Thời gian quay hết số vòng đó là chu kì: T = N/f=531/8=66s

Bài 15: Cho một xe ô tô chạy trên một quãng đường trong 5h. Biết 2h đầu xe chạy với tốc độ trung bình 60km/h và 3h sau xe chạy với tốc độ trung bình 40km/h.Tính tốc trung bình của xe trong suốt thời gian chuyển động.

Hướng dẫn:

→ S₁ = v₁.t₁ = 120 km

→ S₂ = v₂.t₂ = 120 km

$\rightarrow v_{t b}=\frac{S_{1}+S_{2}}{t_{1}+t_{2}}=\frac{120+120}{2+3}=48(k m / h)$

Bài 16: Ô tô chuyển động thẳng từ A → B. Đầu chặng ô tô đi một phần tư tổng thời gian với v = 50km/h. Giữa chặng ô tô đi một phần hai thời gian với v = 40km/h. Cuối chặng ô tô đi một phần tư tổng thời gian với v = 20km/h. Tính vận tốc trung bình của ô tô?

Hướng dẫn:

Quãng đường đi đầu chặng: $S_{1}=v_{1} \cdot \frac{t}{4}=12,5 t$

Quãng đường chặng giữa: $S_{2}=v_{2} \cdot \frac{t}{2}=20 t$

Quãng đường đi chặng cuối: $S_{1}=v_{1} \cdot \frac{t}{4}=5 t$

Vận tốc trung bình: $v_{t b}=\frac{S_{1}+S_{2}+S_{3}}{t}=\frac{12,5 t+20 t+5 t}{t}=37,5(k m / h)$

Bài 17: Một nguời đi xe máy từ Hà Nam về Phủ Lý với quãng đường 45km. Trong nửa thời gian đầu đi với vận tốc v_1,nửa thời gian sau đi với $v_{2}=\frac{2}{3} v_{1}$ . Xác định v_1,v₂biết sau 1h30 phút người đó đến B.

Hướng dẫn:

$\begin{array}{l} s_{1}+s_{2}=50 \Leftrightarrow v_{1} t_{1}+v_{2} t_{2}=50 \\ \text { Mà } t_{1}=t_{2}=\frac{t}{2}=\frac{1,5}{2} \\ \Rightarrow v_{1} \cdot \frac{1,5}{2}+\frac{2}{3} v_{1} \cdot \frac{1,5}{2}=45 \Rightarrow v_{1}=36 \mathrm{km} / \mathrm{h} \Rightarrow v_{2}=24 \mathrm{km} / \mathrm{h} \end{array}$

Bài 18: Một ôtô đi trên con đường bằng phẳng trong thời gian 10 phút với v = 60 km/h, sau đó lên dốc 3 phút với v = 40km/h. Coi ôtô chuyển động thẳng đều. Tính quãng đường ôtô đã đi trong cả giai đoạn.

Hướng dẫn:

$\begin{array}{l} t_{1}=\frac{1}{6}(h) ; t_{2}=\frac{1}{20}(h) \\ \text { Mà } S_{1}=v_{1} \cdot t_{1}=60 \cdot \frac{1}{6}=10(\mathrm{km}) ; S_{2}=v_{2} \cdot t_{2}=2 \mathrm{km} \\ \mathrm{S}=\mathrm{S}_{1}+\mathrm{S}_{2}=10+2=12(\mathrm{km}) \end{array}$

Bài 19: Hai ô tô cùng chuyển động đều trên đường thẳng. Nếu hai ô tô đi ngược chiều thì cứ 20 phút khoảng cách của chúng giảm 30km. Nếu chúng đi cùng chiều thì cứ sau 10 phút khoảng cách giữa chúng giảm 10 km. Tính vận tốc mỗi xe.

Hướng dẫn:

Ta có $t_{1}=30 p h=\frac{1}{3} h ; t_{2}=10 p h=\frac{1}{6} h$

Chọn chiều dương là chiều chuyển động của mỗi xe.

Nếu đi ngược chiều thì S₁ + S₂ = 30

$\Rightarrow\left(v_{1}+v_{2}\right) t_{1}=\left(v_{1}+v_{2}\right) \frac{1}{3}=30 \Rightarrow v_{1}+v_{2}=90\ (1)$

Nếu đi cùng chiêu thì $S_{1}-S_{2}=10$

$\Rightarrow\left(v_{1}-v_{2}\right) t_{2} \Rightarrow \frac{v_{1}-v_{2}}{6}=10 \Rightarrow v_{1}-v_{2}=60\ (2)$

Giải (1) (2) $\Rightarrow$ v₁ = 75km/h; v₂ = 15km/h

Bài 20: Một ôtô chuyển động trên đoạn đường MN. Trong một phần hai quãng đường đầu đi với v = 40km/h. Trong một phần hai quãng đường còn lại đi trong một phần hai thời gian đầu với v = 75km/h và trong một phần hai thời gian cuối đi với v = 45km/h. Tính vận tốc trung bình trên đoạn MN.

Hướng dẫn:

Ta có $s_{1}=\frac{S}{2} \text { Mà } s_{1}=v_{1} \cdot t_{1}=40\ t_{1} \Rightarrow t_{1}=\frac{S}{80}$

Theo bài ra ta có $\mathrm{S}_{2}=\mathrm{S}_{3}+\mathrm{S}_{4}=75\left(\frac{t-t_{1}}{2}\right)+45\left(\frac{t-t_{1}}{2}\right)=60 t-\frac{60 S}{80}$

Mặt khác $S=s_{1}+s_{2}=\frac{S}{2}+60 t-\frac{60 S}{80} \Leftrightarrow 1,25 \mathrm{S}=60 \mathrm{t} \Rightarrow \mathrm{S}=48 \mathrm{t}$

$\Rightarrow V_{t b}=\frac{S}{t}=48 \mathrm{km}$

Bài 21: Một người đi xe máy từ địa điểm A đến địa điểm B cách nhau 4,8km. Nửa quãng đường đầu, xe mấy đi với v₁, nửa quãng đường sau đi với v₂ bằng một phần hai v₁. Xác định v₁, v₂ sao cho sau 15 phút xe máy tới địa điểm B.

Hướng dẫn:

$\begin{array}{l} S_{1}=v_{1} \cdot t_{1} \Rightarrow t_{1}=\frac{S_{1}}{v_{1}}=\frac{S}{2 . v_{1}}=\frac{4800}{2 . v_{1}}=\frac{2400}{v_{1}} \\ S_{2}=v_{2} . t_{2} \Rightarrow t_{2}=\frac{S_{2}}{v_{2}}=\frac{S}{2 . \frac{v_{1}}{2}}=\frac{S}{v_{1}}=\frac{4800}{v_{1}} \\ t_{1}+t_{2}=900 \Rightarrow \frac{2400}{v_{1}}+\frac{4800}{v_{1}}=900 \Rightarrow v_{1}=8(m / s) ; v_{2}=4(m / s) \end{array}$

Bài 22: Một ôtô chạy trên đoạn đường thẳng từ A đến B phải mất khoảng thời gian t. Trong nửa đầu của khoảng thời gian này ô tô có tốc độ là 60km/h. Trong nửa khoảng thời gian cuối ô tô có tốc độ là 40km/h. Tính tốc độ trung bình trên cả đoạn AB.

Hướng dẫn:

Trong nửa thời gian đầu: $S_{1}=v_{1} \cdot t_{1}=60 \cdot \frac{t}{2}=30 t$

Trong nửa thời gian cuối: $S_{2}=v_{2} \cdot t_{2}=40 \cdot \frac{t}{2}=20 t$

$v_{t b}=\frac{S}{t}=\frac{S_{1}+S_{2}}{t_{1}+t_{2}}=\frac{30 t+20 t}{t}=50(k m / h)$

Xem thêm các dạng bài tập Vật Lí hay khác:

30 bài tập về Chuyển động biến đổi đều (2024) có đáp án chi tiết nhất

30 bài tập về Gia tốc và đồ thị vận tốc – thời gian (2024) có đáp án chi tiết nhất

30 bài tập về Độ dịch chuyển và quãng đường đi được (2024) có đáp án chi tiết nhất

30 bài tập về Tốc độ và vận tốc (2024) có đáp án chi tiết nhất

30 bài tập về Chuyển động tổng hợp (2024) có đáp án chi tiết nhất

Được cập nhật 16/11/2023 629 lượt xem

Bởi Thu Trang

Chủ đề: Bài tập vận tốc trung bình

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Vật lí 10

30 bài tập các công thức tính vận tốc trong vật lý 10 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài tập và tóm tắt lý thuyết Vật lí: các công thức tính vận tốc trong vật lý 10 hay, chi tiết cùng với bài tập trắc nghiệm chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Vật lí 10. Mời các bạn đón xem:

124 1 tháng trước

Vật lí 10

30 Bài tập cách cân bằng lực 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài viết gồm bài tập và phương pháp giải Vật lí: cách cân bằng lực hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Vật lí 10 . Mời các bạn đón xem.

136 1 tháng trước

Vật lí 10

30 Bài tập về bài toán ném xiên 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài viết gồm bài tập và phương pháp giải Vật lí: bài toán ném xiên hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Vật lí 10 . Mời các bạn đón xem.

149 1 tháng trước

20 Bài tập vận tốc trung bình (2024) có đáp án

1. Định nghĩa

2. Công thức

3. Kiến thức mở rộng

4. Bài tập vận dụng

Bình luận (0)

Bài viết cùng chủ đề

30 bài tập các công thức tính vận tốc trong vật lý 10 2024 (có đáp án)

30 Bài tập cách cân bằng lực 2024 (có đáp án)

30 Bài tập về bài toán ném xiên 2024 (có đáp án)

Nội dung bài viết