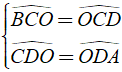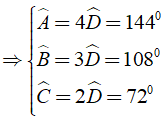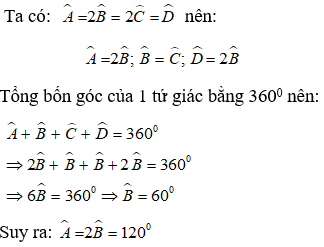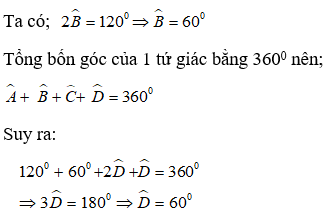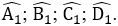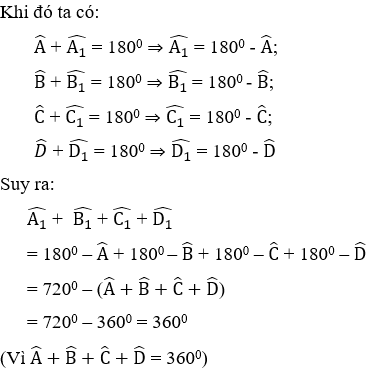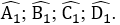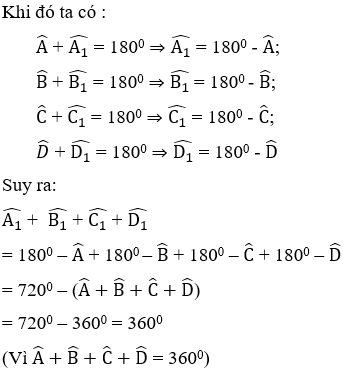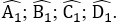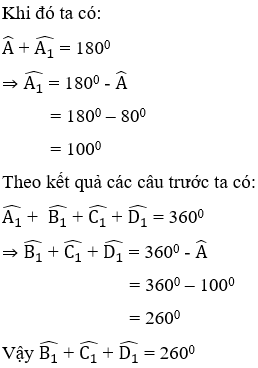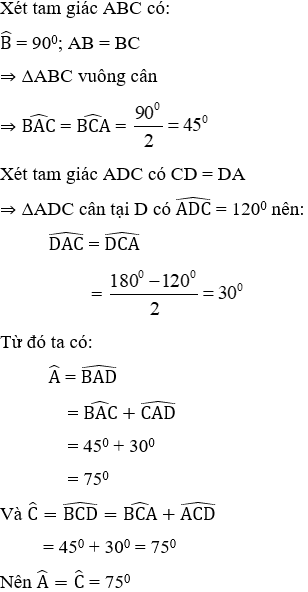20 bài tập Lý thuyết Tứ giác (2024) hay, chi tiết

Tứ giác

Lý thuyết

1. Định nghĩa tứ giác

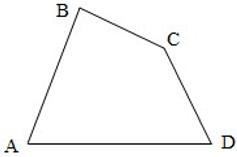
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Chú ý:

   Tứ giác ABCD còn được gọi tên là tứ giác BCDA,ADCB, ... . Các điểm A,B,C,D được gọi là các đỉnh. Các đoạn thẳng AB,BC,CD,DA được gọi là các cạnh.

   Tứ giác ABCD trên hình gọi là tứ giác lồi.

Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

2. Tổng các góc của một tứ giác

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Tổng quát: Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.

Ví dụ: Cho tứ giác ABCD trong đó có Aˆ = 60⁰,Cˆ = 150⁰, Dˆ = 75⁰. Tính số đo của góc Bˆ?

Lời giải:

Theo định lý, tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.

⇔ 60⁰ + Bˆ + 150⁰ + 75⁰ = 360⁰

⇔ Bˆ = 360⁰ - 285⁰ = 75⁰.

Vậy Bˆ = 75⁰.

Bài tập (có đáp án)

Bài tập vận dụng

Bài 1: Cho tứ giác ABCD trong đó Aˆ = 73⁰,Bˆ = 112⁰,Dˆ = 84⁰. Tính số đo góc Cˆ?

Lời giải:

Áp dụng định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ Cˆ = 360⁰ - ( Aˆ + Bˆ + Dˆ ) = 360⁰ - ( 73⁰ + 112⁰ + 84⁰ )

⇒ Cˆ = 360⁰ - 269⁰ = 91⁰.

Vậy số đo của góc Cˆ cần tìm là Cˆ = 91⁰.

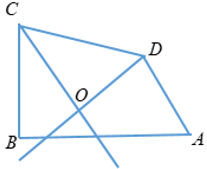
Bài 2: Cho tứ giác ABCD có Aˆ = 70⁰,Bˆ = 90⁰. Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc CODˆ ?

Lời giải:

Áp dụng định lí: Tổng các góc của một tứ giác bằng 360⁰.

Ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ Cˆ + Dˆ = 360⁰ - ( Aˆ + Bˆ ) = 360⁰ - ( 70⁰ + 90⁰ )

⇒ Cˆ + Dˆ = 200⁰

Theo giả thiết, ta có OC, OD là các đường phân giác

Khi đó ta có 

⇒ Cˆ + Dˆ = BCOˆ + OCDˆ + CDOˆ + ODAˆ = 2OCDˆ + 2ODCˆ

⇔ 2( OCDˆ + ODCˆ ) = 200⁰ ⇔ OCDˆ + ODCˆ = 100⁰

Xét Δ OCD có OCDˆ + ODCˆ + CODˆ = 180⁰ ⇒ CODˆ = 180⁰ - ( OCDˆ + ODCˆ ) = 180⁰ - 100⁰ = 80⁰.

Vậy CODˆ = 80⁰.

Bài tập tự luyện

Bài 1: Cho tứ giác ABCD, trong đó Aˆ + Bˆ = 140⁰. Tổng Cˆ + Dˆ = ?

   A. 220⁰   B. 200⁰

   C. 160⁰   D. 150⁰

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ ( Cˆ + Dˆ ) = 360⁰ - ( Aˆ + Bˆ ) = 360⁰ - 140⁰ = 220⁰

Chọn đáp án A.

Bài 2: Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là ?

   A. 120⁰;90⁰;60⁰;30⁰.

   B. 140⁰;105⁰;70⁰;35⁰.

   C. 144⁰;108⁰;72⁰;36⁰.

   D. Cả A, B, C đều sai.

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Theo giải thiết ta có A:B:C:D = 4:3:2:1 ⇒ Aˆ = 4Dˆ;Bˆ = 3Dˆ;Cˆ = 2Dˆ

Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇔ 4Dˆ + 3Dˆ + 2Dˆ + Dˆ = 360⁰

⇔ 10Dˆ = 360⁰ ⇔ Dˆ = 36⁰.

Chọn đáp án C.

Bài 3: Chọn câu đúng trong các câu sau:

   A. Tứ giác ABCD có 4 góc đều nhọn.

   B. Tứ giác ABCD có 4 góc đều tù.

   C. Tứ giác ABCD có 2 góc vuông và 2 góc tù.

   D. Tứ giác ABCD có 4 góc đều vuông.

Lời giải:

Theo định lí: Tổng các góc của một tứ giác bằng 360⁰.

Nhận xét:

+ α là góc nhọn thì 0 < α < 90⁰ ⇒ 0 < 4.α < 360⁰.

⇒ Không tồn tại tứ giác ABCD có 4 góc đều nhọn. ⇒ Loại A.

+ α là góc tù thì 90⁰ < α < 180⁰ ⇒ 360⁰ < 4.α < 720⁰

⇒ Không tồn tại tứ giác ABCD có 4 góc đều tù. ⇒ Loại B.

+ α là góc vuông thì α = 90⁰; β là góc tù thì 90⁰ < β < 180⁰ ⇒ 180⁰ < 2.β < 360⁰

Khi đó ta có : 180⁰ + 180⁰ < 2α + 2β < 180⁰ + 360⁰

⇒ 360⁰ < 2α + 2β < 540⁰

⇒ Không tồn tại tứ giác ABCD có 2 góc nhọn và 2 góc tù. ⇒ Loại C.

+ Vì tứ giác có 4 góc vuông thì tổng các góc bằng 360⁰.

Chọn đáp án D.

Bài 4: Cho tứ giác ABCD có Aˆ = 65⁰;Bˆ = 117⁰;Cˆ = 71⁰. Số đo góc Dˆ = ?

   A. 119⁰.   B. 107⁰.

   C. 63⁰.   D. 126⁰.

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ Dˆ = 360⁰ - ( Aˆ + Bˆ + Cˆ ) = 360⁰ - ( 65⁰ + 117⁰ + 71⁰ )

⇒ Dˆ = 360⁰ - 253⁰ = 107⁰.

Chọn đáp án B.

Bài 5: Cho tứ giác ABCD trong đó có Bˆ = 75⁰;Dˆ = 120⁰. Khi đó Aˆ + Cˆ = ?

   A. 190⁰   B. 130⁰

   C. 215⁰   D. 165⁰

Lời giải:

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ ( Cˆ + Aˆ ) = 360⁰ - ( Bˆ + Dˆ ) = 360⁰ - 195⁰ = 165⁰

Chọn đáp án D.

Bài 6: Xét tứ giác ABCD có Aˆ = Dˆ; Bˆ = 50^o; Cˆ = 90^o . Tính Aˆ

   A. 110^o     B. 100^o

   C. 120^o     D. 90^o

Lời giải:

Chọn đáp án A

Bài 7: Cho tứ giác ABCD có Aˆ = Cˆ = Dˆ = 80^o . Góc Bˆ là góc?

   A. Góc nhọn     B. Góc vuông

   C. Góc tù     D. Góc bẹt

Lời giải:

Chọn đáp án C

Bài 8: Cho tứ giác ABCD có Bˆ + Cˆ = 150^o; Aˆ = Dˆ. Tính góc D?

   A. 105^o     B. 100^o

   C. 120^o     D. 75^o

Lời giải:

Chọn đáp án A

Bài 9: Cho tứ giác ABCD có Aˆ = 2Bˆ = 2Cˆ = Dˆ . Tính số đo góc A?

   A. 90^o     B. 150^o

   C. 120^o     D. 160^o

Lời giải:

Chọn đáp án C

Bài 10: Cho tứ giác ABCD có Aˆ = 2Bˆ = 120^o; Cˆ = 2Dˆ. Tính Dˆ

   A. 45^o     B.90^o

   C. 120^o     D. 60^o

Lời giải:

Chọn đáp án D

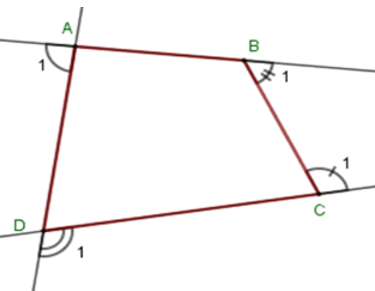
Bài 11: Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là

A. 300⁰       

B. 270⁰       

C. 180⁰       

D. 360⁰

Lời giải

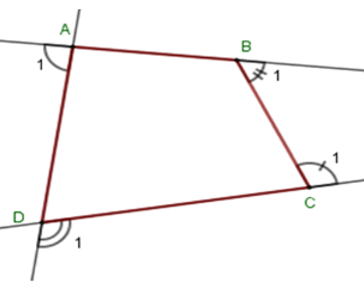
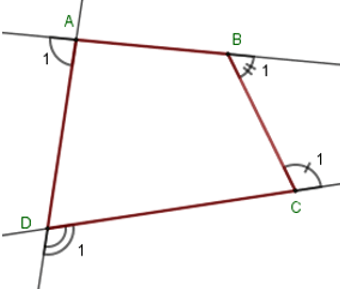
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360⁰.

Đáp án cần chọn là: D

Bài 12: Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 200⁰. Tổng số đo các góc ngoài tại 2 đỉnh A, C là:

A. 160⁰           

B. 260⁰           

C. 180⁰           

D. 100⁰

Lời giải

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360⁰.

Mà tổng số đo góc ngoài tại hai đỉnh B, C bằng 200⁰ nên tổng số đo góc ngoài tại hai đỉnh A, D bằng 360⁰ – 200⁰ = 160⁰.

Đáp án cần chọn là: A

Bài 13: Cho tứ giác ABCD có  = 100⁰. Tổng số đo các góc ngoài đỉnh B, C, D bằng:

A. 180⁰           

B. 260⁰           

C. 280⁰           

D. 270⁰

Lời giải

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Đáp án cần chọn là: C

Bài 14: Cho tứ giác ABCD có  = 80⁰. Tổng số đo các góc ngoài đỉnh B, C, D bằng:

A. 180⁰           

B. 260⁰           

C. 280⁰           

D. 270⁰

Lời giải

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là 

Đáp án cần chọn là: B

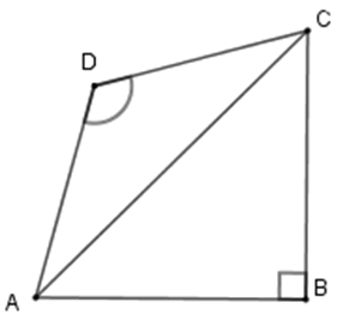
Bài 15: Tứ giác ABCD có AB = BC, CD = DA, 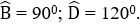 Hãy chọn câu đúng nhất:

Lời giải

Đáp án cần chọn là: D

Xem thêm các dạng bài tập liên quan khác:

50 bài tập về hình bình hành (có đáp án 2024)

50 bài tập về hình thang, hình thang vuông, hình thang cân (có đáp án 2024)

50 bài tập về diện tích hình chữ nhật (có đáp án 2024)

50 bài tập về đa giác, Đa giác lồi, Đa giác đều (có đáp án 2024)

60 Bài tập về hình chóp đều và hình chóp cụt đều (có đáp án năm 2024)