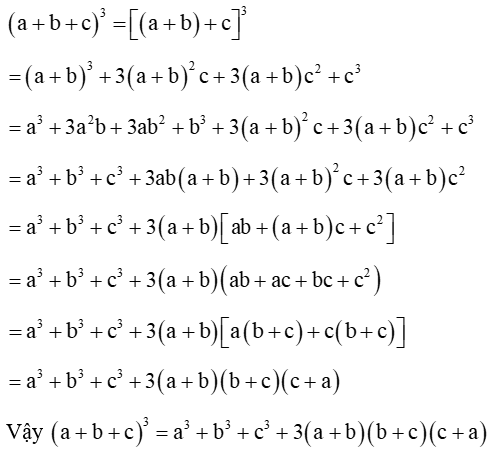Trắc nghiệm Toán 8 Bài 3: Hằng đẳng thức đáng nhớ
A. Trắc nghiệm
Câu 1. Cho biết (3x−1)2+2(x+3)2+11(1+x)(1−x) = ax + b. Khi đó
A. a = 30; b = 6
B. a = – 6; b = –30
C. a = 6; b = 30
D. a = –30; b = –6
Đáp án đúng là: C
Ta có (3x−1)2+2(x+3)2+11(1+x)(1−x)
= (3x)2−2 . 3x . 1+12+2(x2+6x+9)+11(1−x2)
= 9x2−6x+1+2x2+12x+18+11−11x2
= (9x2+2x2−11x2)+(−6x+12x)+(1+18+11)
= 6x + 30
Do đó a = 6; b = 30.
Câu 2. Rút gọn biểu thức M = 4(x+1)2+(2x+1)2−8(x−1)(x+1)−12x, ta được
A. Một số chẵn.
B. Một số chính phương.
C. Một số nguyên tố.
D. Một hợp số.
Đáp án đúng là: C
Ta có M = 4(x+1)2+(2x+1)2−8(x−1)(x+1)−12x
= 4(x2+2x+1)+(4x2+4x+1)−8(x2−1)−12x
= 4x2+8x+4+4x2+4x+1−8x2+8−12x
= (4x2+4x2−8x2)+(8x+4x−12x)+4+1+8
= 13
Vậy M là số nguyên tố.
Câu 3. Giá trị lớn nhất của biểu thức Q = 8 - 8x - x2 là
A. 4
B. – 4
C. 24
D. – 24
Đáp án đúng là: C
Ta có Q = 8 - 8x - x2 = -x2 - 8x - 16 + 16 + 8
= −(x2+8x+16)+24 = −(x+4)2+24
Vì (x+4)2≥0 ∀x∈ℝ nên −(x+4)2≤0 ∀x∈ℝ
Do đó −(x+4)2+24≤24 ∀x∈ℝ
Dấu “=” xảy ra khi x + 4 = 0 khi và chỉ khi x = – 4 .
Vậy giá trị lớn nhất của biểu thức Q là 24 khi x = – 4.
Câu 4. Biểu thức (a + b + c)3 được phân tích thành
A. a3+ b3+ c3+ 3(a + b + c)
B. a3+ b3+ c3+ 3(a + b)(b + c)(c + a)
C. a3+ b3+ c3+ 6(a + b + c)
D. a3+ b3+ c3+ 3(a2+ b2+ c2) + 3(a + b + c)
Đáp án đúng là: B
Câu 5. Cho A = 13+33+53+73+93+113. Khi đó
A. A chia hết cho 12 và 5.
B. A không chia hết cho cả 12 và 5.
C. A chia hết cho 12 nhưng không chia hết cho 5.
D. A chia hết cho 5 nhưng không chia hết cho 12.
Đáp án đúng là: C
A = 13+33+53+73+93+113
= (13+113)+(33+93)+(53+73)
= (1+11)(12−11+112)+(3+9)(32−3 . 9+92)+(5+7)(52−5 . 7+72)
= 12(12−11+112)+12(32−3 . 9+92)+12(52−5 . 7+72)
Vì mỗi số hạng trong tổng đều chia hết cho 12 nên A ⋮ 12
A = 13+33+53+73+93+113
= (13+93)+(33+73)+53+113
= (1+9)(12−9+92)+(3+7)(32−3.7+72)+53+113
= 10(12−9+92)+10(32−3.7+72)+53+113
Ta có: 10(12−9+92) ⋮ 5; 10(32−3.7+72) ⋮ 5; 53 ⋮ 5
Mà 113 không chia hết cho 5 nên A không chia hết cho 5.
Câu 6. Đẳng thức nào sau đây là hằng đẳng thức?
A. x(2x + 1) = 2x2 + x
B. 2x + 1 = x2 + 6
C. x2 - x + 1 = (x + 1)2
D. x + 1 = 3x - 1
Đáp án đúng là: A
Loại đáp án B, C, D vì khi ta thay x = 1 thì hai vế của đẳng thức không bằng nhau.
Ta có x(2x + 1) = x.2 + x.1 = 2x2 + x.
Do đó đẳng thức x(2x + 1) = 2x2 + x là hằng đẳng thức.
Câu 7. Viết biểu thức 25x2 + 20xy + 4y2 dưới dạng bình phương của một tổng.
A. (25x + 4y)2
B. (5x + 2y)2
C. (5x - 2y)(5x + 2y)
D. (25x + 4)2
Đáp án đúng là: B
25x2 + 20xy + 4y2 = (5x)2 + 2.5x.2y + (2y)2 = (5x + 2y)2.
Câu 8. Tìm x, biết: (x - 6)(x + 6) - (x + 3)2 = 9.
A. x = 9
B. x = 1
C. x = – 9
D. x = – 1
Đáp án đúng là: C
(x - 6)(x + 6) - (x + 3)2 = 9
x2 - 62 - (x2 + 6x + 9) = 9
-6x = 9 + 9 + 36
-6x = 54
x = -9
Câu 9. Viết biểu thức 8 + (4x - 3)3 dưới dạng tích
A. (4x - 1)(16x2 - 16x + 1)
B. (4x - 1)(16x2 - 32x + 1)
C. (4x - 1)(16x2 + 32x + 19)
D. (4x - 1)(16x2 - 32x + 19)
Đáp án đúng là: D
8 + (4x - 3)3 = 23 + (4x - 3)3
= (2+4x−3)[22−2.(4x−3)+(4x−3)2]
= (4x−1)(4−8x+6+16x2−24x+9)
= (4x−1)(16x2−32x+19)
Câu 10. Giá trị của biểu thức 125+(x−5)(x3+5x+25) với x = − 5 là
A. 125.
B. −125.
C. 250.
D. −250.
Đáp án đúng là: B
125+(x−5)(x3+5x+25)
= 125 + x3 - 125 = x3.
Thay x = − 5 vào biểu thức, ta có: (-5)3 = -125.
Câu 11. Khai triển hằng đẳng thức (x - 2)3, ta được
A. x3 - 6x2 + 12x - 8
B. x3 + 6x2 + 12x + 8
C. x3 - 6x2 - 12x - 8
D. x3 + 6x2 - 12x + 8
Đáp án đúng là: A
(x - 2)3 = x3−3 . x2 . 2 + 3 . x . 22−23 = x3−6x2+ 12x−8
Câu 12. Tính nhanh: 233 - 9.232 + 27.23 - 27
A. 4000
B. 8000
C. 6000
D. 2000
Đáp án đúng là: B
233 - 9.232 + 27.23 - 27 = 233−3 . 232 . 3 + 3 . 23 . 32−33
= (23 - 3)3 = 203 = 8000
Câu 13. Viết biểu thức (x−3y)(x2+3xy+9y2) dưới dạng hiệu hai lập phương
A. x3 + (3y)3
B. x3 + (9y)3
C. x3 - (3y)3
D. x3 - (9y)3
Đáp án đúng là: C
Ta có: (x−3y)(x2+3xy+9y2)
= (x−3y)[x2+x . 3y+(3y)2]
= x3 - (3y)3
Câu 14. Rút gọn biểu thức (a - b + 1)[a2 + b2 + ab - (a + 2b) + 1] - (a3 + 1), ta được
A. (1 + b)3 - 1
B. (1 + b)3 + 1
C. (1 - b)3 - 1
D. (1 - b)3 + 1
Đáp án đúng là: C
Ta có: (a - b + 1)[a2 + b2 + ab - (a + 2b) + 1] - (a3 + 1)
= [a+(1−b)][a2−(a−ab)+(b2−2b+1)]−(a3+1)
= [a+(1−b)][a2−a(1−b)+(b−1)2]−(a3+1)
= a3+(1−b)3−a3−1 = (1 - b)3 - 1
Câu 15. Tìm x, biết: (x+3)(x2−3x+9)−x(x2−3)=21.
A. x = 2
B. x = – 2
C. x = – 4
D. x = 4
Đáp án đúng là: B
(x+3)(x2−3x+9)−x(x2−3)=21
x3+27−x3+3x=21
3x + 27 = 21
3x = -6
x = -2
Vậy x = -2.
B. Lý thuyết
1. Hằng đẳng thức
Nếu hai biểu thức P và Q nhận giá trị nhưu nhau với mọi giá trị của biến thì ta nói P = Q là một đồng nhất thức hay một hằng đẳng thức
Ví dụ: Đẳng thức 3(x + y) = 3x + 3y là một hằng đẳng thức
2. Hằng đẳng thức đáng nhớ
2.1. Bình phương của một tổng, hiệu
Với hai biểu thức A, B tùy ý, ta có:
(A + B)2 = A2 + 2AB + B2
(A – B)2 = A2 – 2AB + B2
Ví dụ:
• (x + 2)2 = x2 + 2 . x . 2 + 22 = x2 + 4x + 4;
• (x – 2)2 = x2 – 2 . x . 2 + 22 = x2 – 4x + 4.
2.2. Hiệu hai bình phương
Với hai biểu thức A, B tùy ý, ta có:
A2 – B2 = (A – B)(A + B)
Ví dụ: x2 – 36 = ( x – 6)(x + 6)
2.3. Lập phương của một tổng, một hiệu
Với hai biểu thức A, B tùy ý, ta có:
(A + B)3 = A3 + 3A2B + 3AB2 + B3
(A – B)2 = A3 – 3A2B + 3AB2 – B3
Ví dụ:
(x + 1)3 = x3 + 3 . x2 . 1 + 3 . x . 12 + 13
= x3 + 3x2 + 3x + 1
(x – 2)3 = x3 – 3 . x2 . 2 + 3 . x . 22 – 23
= x3 – 6x2 + 12x – 8
2.4. Tổng, hiệu hai lập phương
A3 + B3 = (A + B)(A2 – AB + B2);
A3 – B3 = (A – B)(A2 + AB + B2).
Ví dụ:
• 8 + x3 = 23 + x3 = (2 + x)(22 – 2 . x + x2)
= (2 + x)(4 – 2x + x2).
• 8x3 – y3 = (2x)3 – y3 = (2x – y)[(2x)2 + 2x . y + y2]
= (2x – y)(4x2 + 2xy + y2).
Xem thêm các bài trắc nghiệm Toán 8 Cánh diều hay, có đáp án khác:
Trắc nghiệm Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến
Trắc nghiệm Bài 2: Các phép tính với đa thức nhiều biến
Trắc nghiệm Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử
Trắc nghiệm Bài 1: Phân thức đại số
Trắc nghiệm Bài 2: Phép cộng, phép trừ phân thức đại số