Trắc nghiệm Toán 7 Ôn tập chương 1 có đáp án
Trắc nghiệm Toán 7 Ôn tập chương 1 có đáp án
-
74 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Số đối của ‒3,5 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số đối của số hữu tỉ a, kí hiệu là − a.
Do đó số đối của – 3,5 là – (‒3,5) = 3.5.
Vậy số đối của ‒3,5 là 3,5.
Câu 2:
Hình nào biểu diễn đúng điểm A của số hữu tỉ \[\frac{1}{4}\] trên trục số?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Câu 3:
Để xác định điểm biểu diễn \(\frac{1}{4}\) ta chia đoạn từ điểm 0 đến điểm 1 thành 4 phần bằng nhau. Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 phần sẽ được điểm A.
Do đó trục số của phương án B là đúng.
Hãy sắp xếp các số hữu tỉ sau đây theo thứ tự tăng dần:\(\frac{1}{5},{\rm{ }}\frac{{ - {\rm{ 2}}}}{5},{\rm{ }}\frac{3}{7},{\rm{ }}\frac{{ - {\rm{ 1}}}}{3},{\rm{ }}0.\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có \(\frac{{ - {\rm{ 1}}}}{3}{\rm{ = }}\frac{{ - {\rm{ 5}}}}{{15}}{\rm{, }}\frac{{ - {\rm{ 2}}}}{5}{\rm{ = }}\frac{{ - {\rm{ 6}}}}{{15}}{\rm{; }}\)
Do \(\frac{{ - {\rm{ 5}}}}{{15}}{\rm{ > }}\frac{{ - {\rm{ 6}}}}{{15}}{\rm{ n\^e n 0 > }}\frac{{ - {\rm{ 1}}}}{3}{\rm{ > }}\frac{{ - {\rm{ 2}}}}{5}.\)
\(\frac{3}{7}{\rm{ = }}\frac{{15}}{{35}},{\rm{ }}\frac{1}{5}{\rm{ = }}\frac{7}{{35}};\)
Do \(\frac{{15}}{{35}}{\rm{ > }}\frac{7}{{35}}{\rm{ n\^e n }}\frac{3}{7}{\rm{ > }}\frac{1}{5} > 0.\)
Vậy thứ tự tăng dần của dãy số là: \(\frac{3}{7}{\rm{ > }}\frac{1}{5}{\rm{ > 0 > }}\frac{{ - {\rm{ 1}}}}{3}{\rm{ > }}\frac{{ - {\rm{ 2}}}}{5}.\)
Do đó \(\frac{{ - {\rm{ 2}}}}{5}{\rm{ < }}\frac{{ - {\rm{ 1}}}}{3}{\rm{ < 0 < }}\frac{1}{5}{\rm{ < }}\frac{3}{7}.\)
Vậy sắp xếp các số theo thứ tự tăng dần là: \(\frac{{ - {\rm{ 2}}}}{5}{\rm{; }}\frac{{ - {\rm{ 1}}}}{3}{\rm{; 0; }}\frac{1}{5}{\rm{; }}\frac{3}{7}\).
Câu 4:
Lan muốn mua một chiếc áo nhưng không biết chiều dài của áo tương ứng với các size S, M, L. Người bán hàng cho biết chiều dài áo tương ứng với các size S, M, L lần lượt là 48,5 cm; 50,2 cm; 52,4 cm. Chiếc áo Lan mua phải dài hơn \(\frac{1}{3}\) chiều cao của Lan, biết Lan cao 155 cm. Lan nên mua chiếc áo có size gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Chiếc áo Lan mua cần dài hơn \(\frac{{155}}{3}\) cm;
Ta có: \(48,5{\rm{ = }}\frac{{485}}{{10}};{\rm{ 50,2 = }}\frac{{502}}{{10}};{\rm{ 52,4 = }}\frac{{524}}{{10}};\)
Mà \(\frac{{155}}{3}{\rm{ = }}\frac{{1550}}{{30}};{\rm{ }}\frac{{485}}{{10}}{\rm{ = }}\frac{{1455}}{{30}};{\rm{ }}\)
\(\frac{{502}}{{10}}{\rm{ = }}\frac{{1506}}{{30}};{\rm{ }}\frac{{524}}{{10}}{\rm{ = }}\frac{{1572}}{{30}};\)
Và 1572 > 1550 > 1506 > 1455;
Suy ra \(\frac{{1572}}{{30}}{\rm{ > }}\frac{{1550}}{{30}}{\rm{ > }}\frac{{1506}}{{30}}{\rm{ > }}\frac{{1455}}{{30}};\)
Hay 52,4 > \(\frac{{155}}{3}\) > 50,2 > 48,5.
Vậy Lan nên mua chiếc áo size L.
Câu 5:
Cho số hữu tỉ \(x{\rm{ = }}\frac{{m{\rm{ }} - {\rm{ 2022 }}}}{{2021}}\), với giá trị nào của m thì x là số không dương không âm.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Do x là số hữu tỉ không dương và không âm nên x = 0;
Suy ra \(\frac{{m{\rm{ }} - {\rm{ }}2022}}{{2021}}{\rm{ = 0;}}\)
m – 2022 = 0;
m = 2022.
Vậy m = 2022 thì x là số không dương và không âm.
Câu 6:
Kết luận nào đúng về giá trị của biểu thức \({\rm{A = }}\frac{1}{5}{\rm{ }} - {\rm{ }}\left[ {\left( {\frac{{ - {\rm{ 2}}}}{3}} \right){\rm{ }} - {\rm{ }}\left( {\frac{1}{3}{\rm{ + }}\frac{5}{6}} \right)} \right]?\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(A{\rm{ = }}\frac{1}{5}{\rm{ }} - {\rm{ }}\left[ {\left( {\frac{{ - {\rm{ 2}}}}{3}} \right){\rm{ }} - {\rm{ }}\left( {\frac{1}{3}{\rm{ + }}\frac{5}{6}} \right)} \right]\)
\( = {\rm{ }}\frac{1}{5}{\rm{ }} - {\rm{ }}\left[ {\left( {\frac{{ - {\rm{ 2}}}}{3}} \right){\rm{ }} - {\rm{ }}\left( {\frac{2}{6}{\rm{ + }}\frac{5}{6}} \right)} \right]\)
\( = {\rm{ }}\frac{1}{5}{\rm{ }} - {\rm{ }}\left( {\frac{{ - {\rm{ 2}}}}{3}{\rm{ }} - {\rm{ }}\frac{7}{6}} \right)\)
\( = {\rm{ }}\frac{1}{5}{\rm{ }} - {\rm{ }}\left( {\frac{{ - {\rm{ 4}}}}{6}{\rm{ }} - {\rm{ }}\frac{7}{6}} \right)\)
\( = {\rm{ }}\frac{1}{5}{\rm{ }} - {\rm{ }}\frac{{ - {\rm{ 11}}}}{6}\)
\( = {\rm{ }}\frac{6}{{30}}{\rm{ }} - {\rm{ }}\frac{{ - {\rm{ 55}}}}{{30}}\)
\( = {\rm{ }}\frac{{6{\rm{ }} - {\rm{ }}\left( { - {\rm{ 55}}} \right)}}{{30}}\)![Kết luận nào đúng về giá trị của biểu thức A = 1/5 - [(-2/3) - (1/3 + 5/6)]? (ảnh 1)](https://video.vietjack.com/upload2/images/1655804848/1655805067-image4.png)
\( = {\rm{ }}\frac{{61}}{{30}}.\)
Do \(A{\rm{ }} = {\rm{ }}\frac{{61}}{{30}}{\rm{ }} > {\rm{ }}\frac{{60}}{{30}}{\rm{ }} = {\rm{ }}2\) nên A > 2.
Câu 7:
Số nghịch đảo của số − 0,8 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
Do số nghịch đảo của số hữu tỉ a khác \(0\) là \(\frac{1}{{\rm{a}}}\) nên số nghịch đảo của − 0,8 là: \(\frac{1}{{ - {\rm{ 0,8}}}}{\rm{ = }}\frac{{ - {\rm{ 10}}}}{8}{\rm{ = }}\frac{{ - {\rm{ 5}}}}{4}.\)
Câu 8:
Một ô tô đi từ A đến B với vận tốc 50,5 km/giờ mất 1 giờ 30 phút. Một chiếc xe máy đi với vận tốc bằng \(\frac{5}{6}\) vận tốc của ô tô thì sau bao lâu sẽ đi hết quãng đường AB?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Đổi: 1 giờ 30 phút = 1\(\frac{1}{2}\) giờ = \(\frac{3}{2}\) giờ;
Quãng đường AB dài số km là:
\(50,5{\rm{ }}{\rm{. }}\frac{3}{2}{\rm{ = }}\frac{{101}}{2}{\rm{ }}{\rm{. }}\frac{3}{2}{\rm{ = }}\frac{{303}}{4}\) (km);
Vận tốc của xe máy là:
\(50,5{\rm{ }}{\rm{. }}\frac{5}{6}{\rm{ = }}\frac{{101}}{2}{\rm{ }}{\rm{. }}\frac{5}{6}{\rm{ = }}\frac{{505}}{{12}}\) (km/ giờ);
Thời gian xe máy đi hết quãng đường AB là:
\(\frac{{303}}{4}{\rm{ : }}\frac{{505}}{{12}}{\rm{ = }}\frac{{303}}{4}{\rm{ }}{\rm{. }}\frac{{12}}{{505}}{\rm{ = }}\frac{{3.101}}{4}{\rm{.}}\frac{{3.4}}{{5.101}}{\rm{ = }}\frac{9}{5}\) (giờ).
Câu 9:
Trong bộ số liệu chuẩn, trên thực tế diện tích bề mặt hồ Tây tại Hà Nội là 5,3 km2. Minh thiết kế một bản vẽ có tỉ lệ \(\frac{1}{{150000}}\), xác định diện tích bề mặt của hồ là 0,000004 km2. Số liệu của Minh chênh lệch như thế nào với số liệu chuẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Với số liệu của Minh thì thực tế diện tích bề mặt hồ là:
\(0,000004{\rm{ }}{\rm{. 150000 = }}\frac{4}{{1000000}}{\rm{ }}{\rm{. 150000 = }}\frac{4}{{100}}.15 = \frac{{60}}{{100}}{\rm{ = 0,6 km < 5,3 km}}{\rm{.}}\)
Vậy số liệu của Minh nhỏ hơn số liệu chuẩn.
Câu 10:
Cho hai biểu thức sau, khẳng định nào sau đây đúng?
\(A{\rm{ = }}\frac{{11}}{2}{\rm{ }}{\rm{. 0,62 : }}\left( {\frac{{ - {\rm{ 3}}}}{{100}}} \right);\)\(B{\rm{ = }}\frac{{12}}{{ - {\rm{ 5}}}}{\rm{ : }}\frac{8}{{45}}{\rm{ }}{\rm{. }}\frac{9}{{10}}.\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C.
Ta có: \(A{\rm{ = }}\frac{{11}}{2}{\rm{ }}{\rm{. 0,62 : }}\left( {\frac{{ - {\rm{ 3}}}}{{100}}} \right)\)
\( = {\rm{ }}\frac{{11}}{2}{\rm{ }}{\rm{. }}\frac{{62}}{{100}}{\rm{ }}{\rm{. }}\left( {\frac{{{\rm{ 100}}}}{{ - 3}}} \right)\)
\[ = {\rm{ }}\frac{{11}}{2}{\rm{ }}{\rm{. }}\frac{{31}}{{50}}{\rm{ }}{\rm{. }}\left( {\frac{{ - 100}}{3}} \right)\]
\( = {\rm{ }}\frac{{341}}{{100}}{\rm{ }}{\rm{. }}\left( {\frac{{ - {\rm{ 100}}}}{3}} \right){\rm{ = }}\frac{{ - {\rm{ 341}}}}{3};\)
\(B{\rm{ = }}\frac{{12}}{{ - {\rm{ 5}}}}{\rm{ : }}\frac{8}{{45}}{\rm{ }}{\rm{. }}\frac{9}{{10}}\)
\( = {\rm{ }}\frac{{12}}{{ - {\rm{ 5}}}}{\rm{ }}{\rm{. }}\frac{{45}}{8}{\rm{ }}{\rm{. }}\frac{9}{{10}}\)
\( = {\rm{ }}\frac{3}{{\rm{1}}}{\rm{ }}{\rm{. }}\frac{{ - 9}}{2}{\rm{ }}{\rm{. }}\frac{9}{{10}}\)
\( = {\rm{ }}\frac{{ - {\rm{ 27}}}}{2}{\rm{ }}{\rm{. }}\frac{9}{{10}}{\rm{ = }}\frac{{ - {\rm{ 243}}}}{{20}}.\)
Mà \(\frac{{ - {\rm{ 341}}}}{3}{\rm{ < }}\frac{{ - {\rm{ 300}}}}{3}{\rm{ = }} - {\rm{ 100;}}\)
\( - {\rm{ 100 = }}\frac{{ - {\rm{ 2000}}}}{{20}}{\rm{ < }}\frac{{ - {\rm{ 243}}}}{{20}}.\)
Suy ra \(\frac{{ - {\rm{ 341}}}}{3}{\rm{ < }}\frac{{ - {\rm{ 243}}}}{{20}}.\)
Vậy chọn đáp án C.
Câu 11:
Chọn khẳng định đúng về quy tắc chuyển vế đối với số hữu tỉ:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quy tắc chuyển vế đối với số hữu tỉ tương tự đối với số nguyên: khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.
Câu 12:
Giá trị của x1 bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C.
Ta có: xn là tích của n thừa số x nên quy ước x1 = x.
Câu 13:
64 là lũy thừa của số tự nhiên nào và có số mũ bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
Ta có:
Lũy thừa của cơ số 3 và số mũ bằng 5 là:
35 = 3 . 3 . 3 . 3 . 3 = 243;
Lũy thừa của 2 và số mũ bằng 6 là:
26 = 2 . 2 . 2 . 2 . 2 . 2 = 64;
Lũy thừa của 3 và số mũ bằng 4 là:
34 = 3 . 3 . 3 . 3 = 81;
Lũy thừa của 2 và số mũ bằng 5 là:
25 = 2 . 2 . 2 . 2 . 2 = 32.
Vậy 64 là lũy thừa của cơ số là 2 và số mũ bằng 6.
Câu 14:
Chọn đáp án sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D.
Ta có: 20220 = 1, suy ra đáp án A đúng;
(− 7)3 . (− 7)3 = (− 7)3 + 3 = (− 7)6, suy ra đáp án B đúng;
37 : 35 = 37 – 5 = 32 = 9, suy ra đáp án C đúng;
(93)3 = 93 . 3 = 99, suy ra đáp án D sai.
Câu 15:
So sánh hai lũy thừa: 122 và 212.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Ta có: 122 = 12 . 12 = 144;
212 = 26 + 6 = 26 . 26 = 64 . 64 = 4096.
Do 144 < 4096 nên 122< 212
Câu 16:
Chọn đáp án sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C.
3 . 43 là tích của 3 với lập phương của 4 (Đúng).
343 là lũy thừa với cơ số là 34 (Đúng).
(3 . 4)3 là lũy thừa với cơ số là 3 (Sai);
Cơ số của (3 . 4)3 được xác định bởi phép tính trong dấu ngoặc, tức là 3 . 4 = 12.
(3 . 4)3 là lũy thừa với cơ số là 12 (Đúng).
Câu 17:
Một chiếc mâm đồng có bán kính r = 19,5 cm và một chiếc đĩa đồng có bán kính R = 6,5 cm. Hỏi diện tích của chiếc mâm gấp bao nhiêu lần diện tích chiếc đĩa?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Công thức tính diện tích hình tròn có bán kính R là: S = π . R2.
Diện tích bề mặt chiếc mâm là:
π . r2 = π . 19,52 = π . \({\left( {\frac{{39}}{2}} \right)^2}\) = π . \(\frac{{1521}}{4}\) (cm2);
Diện tích bề mặt chiếc đĩa là:
\(\pi \) . R2 = \(\pi \) . 6,52 = \(\pi \) . \({\left( {\frac{{13}}{2}} \right)^2}\) = \(\pi \) . \(\frac{{169}}{4}\) (cm2);
Diện tích của chiếc mâm gấp diện tích chiếc đĩa số lần là:
 \(\frac{{\pi {\rm{ }}{\rm{. }}\frac{{1521}}{4}}}{{\pi {\rm{ }}{\rm{. }}\frac{{169}}{4}}}{\rm{ = }}\frac{{1521}}{4}{\rm{ }}{\rm{. }}\frac{4}{{169}}{\rm{ = }}\frac{{1521}}{{169}}{\rm{ = 9}}\) (lần).
\(\frac{{\pi {\rm{ }}{\rm{. }}\frac{{1521}}{4}}}{{\pi {\rm{ }}{\rm{. }}\frac{{169}}{4}}}{\rm{ = }}\frac{{1521}}{4}{\rm{ }}{\rm{. }}\frac{4}{{169}}{\rm{ = }}\frac{{1521}}{{169}}{\rm{ = 9}}\) (lần).
Vậy diện tích chiếc mâm gấp 9 lần diện tích chiếc đĩa.
Câu 18:
Trong chân không, vận tốc ánh sáng là 299 792 458 m/s; với các tính toán không cần độ chính xác cao ta có thể coi vận tốc ánh sáng là 3.108 m/s. Trong một nghiên cứu, ánh sáng từ một ngôi sao đến Trái Đất mất 10 phút 20 giây. Khoảng cách giữa ngôi sao đó đến Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đổi 10 phút 13 giây = 613 giây;
Khoảng cách giữa ngôi sao và Trái Đất là:
613 . 3 . 108 = 1839 . 108 (m) = 1839 . 105 (km)
Vậy khoảng cách giữa ngôi sao đó đến Trái Đất xấp xỉ bằng 1839 . 105 km.
Câu 19:
Trong các phép tính của số hữu tỉ, thứ tự thực hiện phép tính đối với biểu thức không có dấu ngoặc là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B.
Thứ tự thực hiện các phép tính đối với số hữu tỉ tương tự thứ tự thực hiện các phép tính đối với số tự nhiên, số nguyên, phân số, số thập phân trong trường hợp biểu thức không có dấu ngoặc: Lũy thừa → Nhân và chia → Cộng và trừ.
Câu 20:
Tìm x, biết: \(2x{\rm{ }} - {\rm{ }}{\left( {\frac{2}{3}} \right)^2}{\rm{ = }}\frac{5}{9}.\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Ta có: \(2x{\rm{ }} - {\rm{ }}{\left( {\frac{2}{3}} \right)^2}{\rm{ = }}\frac{5}{9}\)
\(2x{\rm{ }} - {\rm{ }}\frac{4}{9}{\rm{ = }}\frac{5}{9}\)
\(2x{\rm{ = }}\frac{5}{9}{\rm{ + }}\frac{4}{9}\)
\(2x = {\rm{ }}\frac{9}{9}\)
2x = 1
\(x{\rm{ = }}\frac{1}{2}{\rm{ }}\)
x = 0,5.
Vậy x = 0,5.
Câu 21:
Khi bỏ dấu ngoặc trong biểu thức − (− a + b − 5 − c) ta được kết quả là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C.
Khi bỏ dấu ngoặc có dấu “−” đằng trước, ta đổi dấu của các số hạng trong dấu ngoặc: dấu “+” đổi thành dấu “−” và dấu “−” đổi thành dấu “+”.
Vậy − (− a + b − 5 − c) = a – b + 5 + c.
Câu 22:
Tìm x, biết: x + (− x + 3) – (x − 7) = 9.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A.
Ta có: x + (− x +3) – (x −7) = 9
x − x +3 – x + 7 = 9
(3 + 7) + (x – x – x) = 9
10 + (‒ x) = 9
10 – x = 9
x = 10 – 9
x = 1.
Vậy x = 1.
Câu 23:
Lan mang một số tiền dự định mua 4 quyển vở về viết. Do có đợt giảm giác nên với cùng số tiền đó Lan đã mua được 5 quyển vở với giá đã giảm là 12 000 đồng mỗi quyển. Giá tiền ban đầu khi chưa giảm giá của mỗi quyển vở là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Lan mang theo số tiền dự định mua vở là:
12 000 . 5 = 60 000 (đồng)
Giá tiền ban đầu khi chưa giảm giá của một quyển vở là:
60 000 : 4 = 15 000 (đồng)
Câu 24:
Trong đợt tri ân khách hàng của một cửa hàng điện máy xanh, cửa hàng giảm 20% giá niêm yết cho mỗi một sản phẩm tivi LG. Cửa hàng vẫn lãi 10% của giá nhập về đối với mỗi chiếc tivi bán ra. Giá niêm yết của một chiếc tivi là bao nhiêu, biết rằng mỗi sản phẩm tivi bán ra thì cửa hàng lãi được 800 000 đồng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Sau khi bán với giá khuyến mãi thì cửa hàng lãi 10% được 800 000 đồng giá nhập của mỗi chiếc ti vi là: 800 000 : \(\frac{{10}}{{100}}\) = 800 000 . \(\frac{{100}}{{10}} = \) 800 000 . 10 = 8 000 000 (đồng)
Khi đó giá bán khuyến mãi của mỗi chiếc tivi là: 8 000 000 + 800 000 = 8 800 000 (đồng)
Vì cửa hàng giảm giá 20% so với giá niêm yết nên giá sản phẩm được bán ra bằng 80% giá niêm yết, do đó giá niêm yết của mỗi chiếc ti vi là:
\({\rm{8 800 000 : }}\frac{{80}}{{100}}\)= \(8{\rm{ }}800{\rm{ 000 }}{\rm{. }}\frac{{100}}{{80}}{\rm{ = 11 000 000}}\) (đồng)
Vậy giá niêm yết của mỗi chiếc tivi là 11 triệu đồng.
Câu 25:
Anh Minh kinh doanh hoa quả nhập khẩu. Trong lần nhập hàng vừa qua anh đã bỏ ra 90 000 000 đồng để nhập lô hàng mới. Nhưng do quá trình vận chuyển không được đảm bảo nên \(\frac{1}{3}\) số hàng nhập về không đảm bảo chất lượng. Anh Minh đã bán số hàng còn lại cao hơn 10% so với giá nhập vào và số hàng không đảm bảo chất lượng thấp hơn 15% so với giá nhập vào. Hỏi doanh thu lô hàng mới của anh Minh là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số tiền nhập hàng không đảm bảo chất lượng là:
\(\frac{1}{3}{\rm{ }}.{\rm{ }}90{\rm{ }}000{\rm{ 000 }} = {\rm{ 30 000 }}000\) (đồng)
Số tiền nhập hàng đảm bảo chất lượng là: 90 000 000 – 30 000 000 = 60 000 000 (đồng)
Số tiền anh Minh thu được khi bán hàng đảm bảo chất lượng là:
60 000 000 . (100% + 10%) = \(60{\rm{ }}000{\rm{ 000 }}.\,{\rm{ }}\frac{{110}}{{100}} = {\rm{ }}66{\rm{ }}000{\rm{ }}000\) (đồng)
Số tiền anh Minh thu được khi bán hàng không đảm bảo chất lượng là:
30 000 000. (100% ‒ 15%) = \(30{\rm{ }}000{\rm{ }}000.\frac{{85}}{{100}}{\rm{ }} = {\rm{ }}25{\rm{ }}500{\rm{ }}000\) (đồng)
Vậy doanh thu lô hàng mới của anh Minh là:
66 000 000 + 25 500 000 = 91 500 000 đồng.
Vậy doanh thu lô hàng mới của anh Minh là 91 500 000 đồng.
Câu 26:
Dạng viết gọn của 0,2333… là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta thấy trong hàng thập phân của số 0,2333… có chữ số 3 xuất hiện liên tiếp mãi bắt đầu từ hàng trăm nên số 3 là chu kì của số thập phân vô hạn tuần hoàn 0,2333… và số thập phân đó được viết gọn là 0,2(3).
Vậy 0,2333 = 0,2(3).
Câu 27:
Số thập phân 0,005 biểu diễn dưới dạng phân số tối giản nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \(0,005{\rm{ = }}\frac{5}{{1000}}{\rm{ = }}\frac{1}{{200}}.\)
Vậy số thập phân 0,005 biểu diễn dưới dạng phân số tối giản là \(\frac{1}{{200}}.\)
Câu 28:
Biết m là một số thập phân vô hạn tuần hoàn và 2,347923 < m < 2,4452347. Tìm m?
</>
 Xem đáp án
Xem đáp án
Đáp án đúng là: C.
Ta có: 2(3) = 2,333… < 2,347923 do đó m = 2,(3) là sai.
2,(34) = 2,343434… < 2,347923 do đó m = 2,(34) là sai.
2,347923 < 2,444… < 2,4452347 do đó m = 2,(4) là đúng.
2,445445445… > 2,4452347 do đó m = 2,(445) là sai.
Vậy m = 2,(4).
</></></>
Câu 29:
Cho biểu đồ biểu diễn kết quả học tập của học sinh khối 7.
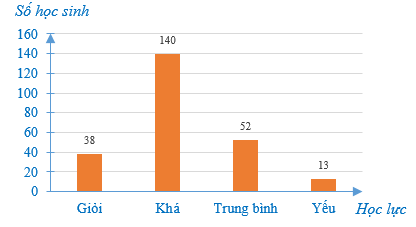
Số học sinh học lực Trung bình ít hơn số học sinh học lực Khá bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số học sinh Khá là 140 và số học sinh Trung bình là 52.
Số học sinh học lực Trung bình ít hơn số lượng học sinh học lực Khá là:
140 – 52 = 88 (học sinh)
Vậy số học sinh học lực Trung bình ít hơn số học sinh học lực Khá là 88 học sinh.
Câu 30:
Dưới đây là biểu đồ biểu chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:
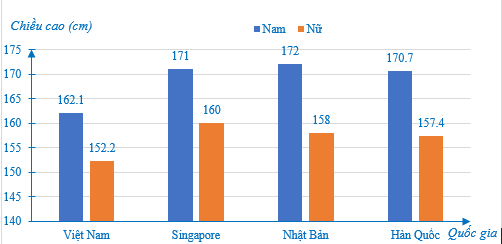
Sự chênh lệch chiều cao giữa nam và nữ ở nước nào lớn nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Chênh lệch chiều cao giữa nam và nữ ở:
Việt Nam là 162,1 – 152,2 = 9,9 (cm);
Singapore là 171 – 160 = 11 (cm);
Nhật Bản là 172 – 158 = 14 (cm);
Hàn Quốc là 170,7 – 157,4 = 13,3 (cm).
Vậy sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là lớn nhất.
