Trắc nghiệm Toán 6 KNTT Bài 5: Các dạng toán về phép phép nhân và phép chia số tự nhiên có đáp án
Dạng 1: Thực hiện phép nhân, phép chia các số tự nhiên có đáp án
-
155 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 2:
Tích 25.9676.4 có giá trị bằng kết quả của phép tính nào dưới đây?
Xem đáp án
Đáp án đúng là: C
25.9676.4 = (25.4).9676 = 100.9676 = 9676.100
Câu 3:
Kết quả của phép tính \[2012.2a + 2012.5a + 2012.3a\] là
Xem đáp án
Đáp án đúng là: C
\[2012.2a + 2012.5a + 2012.3a\]
= 2012a.(2 + 5 + 3) = 2012a.10 = 20120a
Câu 4:
Hãy so sánh \[A = 657.1982\] và \[B = 660.1952\]
Xem đáp án
Đáp án đúng là: A
\[A = 657.1982\] = 657.(1952 + 30) = 657.1952 + 657.30 = 657.1952 + 19 710
\[B = 660.1952\]= (657 + 3).1952 = 657.1952 + 3.1952 = 657.1952 + 5 856
Mà 19710 > 5 856 nên A > B
Câu 5:
Tích 1.3.5.7....97 có
Xem đáp án
Đáp án đúng là: B
Tích của một số tự nhiên có chữ số tận cùng là 5 với một số tự nhiên chẵn sẽ có chữ số tận cùng là 0.
Tích của một số tự nhiên có chữ số tận cùng là 5 với một số tự nhiên lẻ sẽ có chữ số tận cùng là 5.
Tích \[1.3.5.7....97\] là tích các số tự nhiên lẻ liên tiếp trong đó có số 5 nên tích có chữ số tận cùng là chữ số 5.
Câu 6:
Tính nhanh: \[769:15 + 731:15\]
Xem đáp án
Đáp án đúng là: A
\[769:15 + 731:15\] = (769 + 731):15 = 1500:15 = 100.
Câu 7:
Biết \(0 \le x < 100\). Tích các số tự nhiên x là
Xem đáp án
Đáp án đúng là: C
Số tự nhiên x thỏa mãn \(0 \le x < 100\) nên \(x \in \){0; 1; 2; 3; …; 99}.
Tích các số tự nhiên x là:
0.1.2.3. … .99 = 0 (vì trong các thừa số có một thừa số 0).
Câu 10:
Tìm thương và số dư (nếu có) của phép chia 2059:17
Xem đáp án
Đáp án đúng là: B
Đặt tính, ta có:
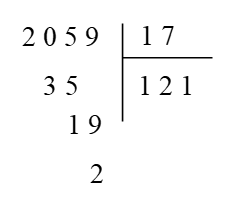
Vậy 2 059:17 = 121 (dư 2).