5 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 CTST Bài 2. Xác suất của biến cố (Vận dụng) có đáp án

Câu 1:

Có ba chiếc hộp. Mỗi hộp chứa 5 tấm thẻ được đánh số từ 1 đến 5. Lấy ngẫu nhiên từ mỗi hộp một thẻ rồi cộng các số trên 3 tấm thẻ vừa rút ra lại với nhau. Xác suất để kết quả thu được là số chẵn là:

A. $\frac{1}{6}$

B. $\frac{99}{125}$

C. $\frac{1}{2}$

D. $\frac{26}{125}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

⦁ Ta tìm số phần tử của không gian mẫu:

Giai đoạn 1: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ nhất, ta có $C_{5}^{1}$ cách chọn.

Giai đoạn 2: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ hai, ta có $C_{5}^{1}$ cách chọn.

Giai đoạn 3: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ ba, ta có $C_{5}^{1}$ cách chọn.

Theo quy tắc nhân, ta có tất cả $C_{5}^{1} . C_{5}^{1} . C_{5}^{1} = 125$ cách chọn.

Do đó n(Ω) = 125.

⦁ Tính số phần tử của biến cố theo yêu cầu bài toán:

Gọi A: “Kết quả thu được là số chẵn”.

Trường hợp 1: 2 thẻ là số lẻ (trong {1; 3; 5}) và 1 thẻ là số chẵn (trong {2; 4}).

Khi đó ta có $C_{3}^{1} . C_{3}^{1} . C_{2}^{1} = 18$ cách chọn.

Trường hợp 2: Cả 3 thẻ đều là số chẵn.

Khi đó ta có $C_{2}^{1} . C_{2}^{1} . C_{2}^{1} = 8$ cách chọn.

Kết hợp cả hai trường hợp, ta được n(A) = 18 + 8 = 26.

Vậy xác suất của biến cố A là: $P (A) = \frac{n (A)}{n (Ω)} = \frac{26}{125}$ .

Ta chọn phương án D.

Câu 2:

Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Xác suất để 1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai là:

A. $\frac{3}{4}$

B. $\frac{3}{16}$

C. $\frac{13}{16}$

D. $\frac{1}{4}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Không gian mẫu của phép thử trên là số cách xếp 4 hành khách lên 4 toa tàu.

Vì chọn mỗi hành khách có 4 cách chọn toa nên ta có 4⁴ cách xếp.

Suy ra số phần tử của không gian mẫu là n(Ω) = 4⁴.

Gọi biến cố A: “1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai”.

Để tìm số phần tử của biến cố A, ta chia thành hai giai đoạn như sau:

Giai đoạn 1: Chọn 3 hành khách trong số 4 hành khách và chọn 1 toa trong số 4 toa.

Sau đó xếp lên toa đó 3 hành khách vừa chọn.

Khi đó ta có $C_{4}^{3} . C_{4}^{1}$ cách.

Giai đoạn 2: Chọn 1 toa trong số 3 toa còn lại và xếp 1 hành khách còn lại lên toa đó.

Suy ra có $C_{3}^{1}$ cách. Hiển nhiên khi đó 2 toa còn lại sẽ không có hành khách nào.

Theo quy tắc nhân, ta có n(A) = $C_{4}^{3} . C_{4}^{1} . C_{3}^{1}$ .

Vậy xác suất của biến cố A là: $P (A) = \frac{n (A)}{n (Ω)} = \frac{C_{4}^{3} . C_{4}^{1} . C_{3}^{1}}{4^{4}} = \frac{3}{16}$ .

Ta chọn phương án B.

Câu 3:

Đề cương ôn tập cuối năm môn Toán lớp 10 có 30 câu hỏi. Đề thi thử cuối năm gồm 3 câu hỏi trong số 30 câu hỏi trong đề cương. Một học sinh chỉ ôn 20 câu trong đề cương. Giả sử các câu hỏi trong đề cương đều có khả năng được chọn làm câu hỏi trong đề thi cuối năm như nhau. Khi đó xác suất để có ít nhất 2 câu hỏi của đề thi cuối năm nằm trong số 20 câu hỏi mà học sinh nói trên đã ôn là:

A. $\frac{152}{203}$

B. $\frac{51}{203}$

C. $\frac{3}{46}$

D. $\frac{43}{46}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Chọn ngẫu nhiên 3 câu hỏi trong số 30 câu hỏi trong đề cương để làm đề thi (không tính đến thứ tự) thì có $C_{30}^{3} = 4 060$ cách chọn.

Do đó số phần tử của không gian mẫu là: n(Ω) = 4 060.

Gọi biến cố M: “Có ít nhất 2 câu hỏi của đề thi cuối năm nằm trong số 20 câu hỏi đã ôn”.

Ta thấy sẽ xảy ra một trong hai trường hợp sau:

Trường hợp 1: Trong đề thi có đúng 2 câu hỏi trong số 20 câu học sinh đã ôn.

Chọn ngẫu nhiên 2 câu hỏi trong số 20 câu đã ôn (không tính đến thứ tự) thì có $C_{20}^{2}$ cách chọn.

Chọn ngẫu nhiên 1 câu hỏi còn lại trong 10 câu chưa ôn thì có $C_{10}^{1}$ cách chọn.

Suy ra trường hợp 1 có $C_{20}^{2} . C_{10}^{1}$ cách chọn.

Trường hợp 2: Trong đề thi có cả 3 câu hỏi trong số 20 học sinh đã ôn.

Chọn ngẫu nhiên 3 câu hỏi trong số 20 câu đã ôn (không tính đến thứ tự) thì có $C_{20}^{3}$ cách chọn.

Kết hợp cả hai trường hợp trên, ta có $n (A) = C_{20}^{2} . C_{10}^{1} + C_{20}^{3} = 3 040$ .

Vậy xác suất của biến cố A là: $P (A) = \frac{n (A)}{n (Ω)} = \frac{3 040}{4 060} = \frac{152}{203}$ .

Ta chọn phương án A.

Câu 4:

Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Xác suất để phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt là:

A. $\frac{2}{3}$

B. $\frac{5}{6}$

C. $\frac{1}{3}$

D. $\frac{1}{2}$

Xem đáp án

`Hướng dẫn giải

Đáp án đúng là: A

Số phần tử của không gian mẫu là: n(Ω) = 6.

Gọi K: “Phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt”.

Ta có ∆ = b² – 8.

$\Leftrightarrow [\begin{array}{l} b < - 2 \sqrt{2} \\ b > 2 \sqrt{2} \end{array}$

Phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt khi và chỉ khi ∆ > 0

⇔ b² – 8 > 0

Lại có xúc xắc xuất hiện mặt b chấm nên b ∈ {1; 2; 3; 4; 5; 6}.

Do đó ta nhận b ∈ {3; 4; 5; 6}.

Suy ra n(K) = 4.

Vậy xác suất của biến cố K là: $P (K) = \frac{n (K)}{n (Ω)} = \frac{4}{6} = \frac{2}{3}$ .

Ta chọn phương án A.

Câu 5:

Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tọa độ các đỉnh A(–2; 0), B(–2; 2), C(4; 2), D(4; 0). Chọn ngẫu nhiên một điểm có tọa độ (x; y) (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD, kể cả các điểm nằm trên cạnh. Gọi A là biến cố “x, y đều chia hết cho 2”. Xác suất của biến cố A là:

A. $\frac{7}{21}$

B. $\frac{13}{21}$

C. 1

D. $\frac{8}{21}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

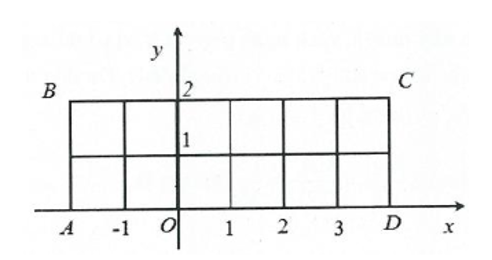
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tọa độ các đỉnh (ảnh 1)

Ta có Ω = {(x; y) | x, y ∈ ℤ; –2 ≤ x ≤ 4 và 0 ≤ y ≤ 2}.

Khi đó x ∈ {–2; –1; 0; 1; 2; 3; 4} và y ∈ {0; 1; 2}.

Chọn 1 hoành độ có 7 cách chọn và chọn 1 tung độ có 3 cách chọn.

Áp dụng quy tắc nhân, ta suy ra n(Ω) = 7.3 = 21 (mỗi điểm là một giao điểm trên hình).

Ta có A: “x, y đều chia hết cho 2”.

Suy ra A = {(x; y) | x ∈ {–2; 0; 2; 4} và y ∈ {0; 2}}.

Chọn 1 hoành độ (chia hết cho 2) có 4 cách chọn và chọn 1 tung độ (chia hết cho 2) thì có 2 cách chọn.

Theo quy tắc nhân, ta có n(A) = 4.2 = 8.

Vậy xác suất của biến cố A là: $P (A) = \frac{n (A)}{n (Ω)} = \frac{8}{21}$ .

Ta chọn phương án D.

Trắc nghiệm Toán 10 CTST Bài 2. Xác suất của biến cố (Phần 2) có đáp án

Trắc nghiệm Toán 10 CTST Bài 2. Xác suất của biến cố (Vận dụng) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương