Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án
Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án
-
1034 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tam giác ABC có . Số đo góc bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có: .
Do đó, .
Câu 2:
Tam giác ABC có và . Tính độ dài cạnh BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo định lí hàm cosin, ta có:
.Câu 3:
Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và . Tính độ dài cạnh cạnh BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
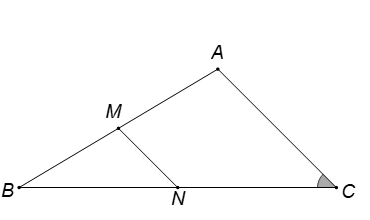
Gọi M, N lần lượt là trung điểm của AB, BC.
MN là đường trung bình của .
. Mà MN = 3, suy ra AC = 6.
Theo định lí hàm cosin, ta có:
- 6.BC - 45 = 0
BC = 3 + 3
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo định lí hàm cosin, ta có:
- .BC + 1 = 0
.
Câu 5:
Tam giác ABC có và AB = 5. Tính độ dài cạnh AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo định lí hàm sin, ta có:
.Câu 6:
Cho hình thoi ABCD cạnh bằng 1cm và có . Tính độ dài AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
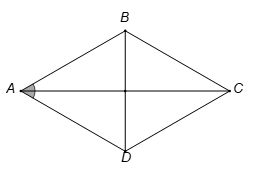
Do ABCD là hình thoi, có .
Theo định lí hàm cosin, ta có:
Câu 7:
Tam giác ABC có . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM..
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
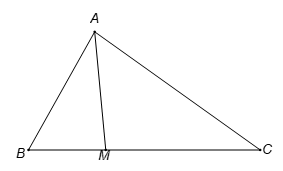
Theo định lí hàm cosin, ta có : .
Do . Theo định lí hàm cosin, ta có:
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
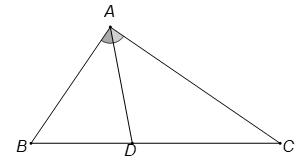
Theo định lí hàm cosin, ta có:
Trong có .
Câu 9:
Tam giác ABC có và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Áp dụng định lí Cosin, ta có
Suy ra tam giác ABC vuông tại B do đó bán kính
Câu 10:
Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc bằng nhau. Đặt . Trong các hệ thức sau, hệ thức nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
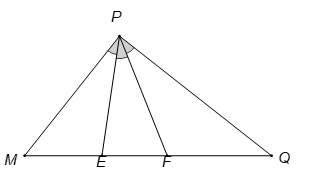
Ta có: .
Theo định lí hàm cosin, ta có:
Câu 11:
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
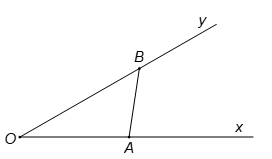
Theo định lí hàm sin, ta có:
Do đó, độ dài OB lớn nhất khi và chỉ khi
.
Khi đó OB = 2.
Câu 12:
Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
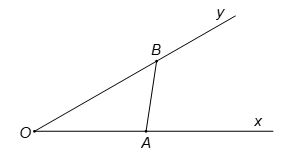
Theo định lí hàm sin, ta có:
Do đó, độ dài OB lớn nhất khi và chỉ khi: .
Khi đó OB = 2. Tam giác OAB vuông tại .
Câu 13:
Tam giác ABC có . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức . Khi đó góc bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có: .
Mà
(do )
Khi đó, .
Câu 14:
Tam giác ABC vuông tại A, có . Gọi m là độ dài đoạn phân giác trong góc . Tính m theo b và c.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: .
Do AD là phân giác trong của
.
Theo định lí hàm cosin, ta có:
hay .
Câu 15:
Tam giác ABC có BC = 10 và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Áp dụng định lí sin, ta có:
