Trắc nghiệm Quan hệ chia hết. Tính chất chia hết có đáp án ( Nhận biết )
Trắc nghiệm Quan hệ chia hết. Tính chất chia hết có đáp án ( Nhận biết )
-
64 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Với a, b là hai số tự nhiên, b ≠ 0.
Nếu có số tự nhiên q sao cho a = b . q thì ta nói a chia hết cho b, khi đó a là bội của b và b là ước của a.
Vậy đáp án A, B, D đúng và C là sai.
Chọn đáp án C.
Câu 2:
Xem đáp án
Ta có: 12 chia hết cho 12 nên 12 cũng là một ước của chính nó.
Lại có 12 không chia hết cho các số 5, 8, 24 nên các số này không là ước của 12.
Chọn đáp án C.
Câu 3:
Xem đáp án
Theo tính chất chia hết của một tổng, một hiệu và một tích thì các đáp án A, B, C là đúng và đáp án D là sai.
Chọn đáp án D.
Câu 4:
Xem đáp án
Nhận thấy các số 12, 1, 23 không chia hết cho 7 nên các số này không thể là bội của 7.
Lại có 49 : 7 = 7 nên 49 chia hết cho 7, do đó 49 là một bội của 7.
Chọn đáp án C.
Câu 5:
Xem đáp án
Với a là một số tự nhiên khác 0 thì ta có:
+ a là ước của a (vì a : a = 1 nên a chia hết cho a)
+ a là bội của a (vì a chia hết cho a)
+ 0 là bội của a (vì 0 : a = 0 nên 0 chia hết cho a)
Vậy cả ba đáp án A, B, C đều đúng.
Chọn đáp án D.
Câu 6:
Xem đáp án
Nhận thấy các số 0, 8, 32 đều chia hết cho 4 nên 0, 8, 32 đều là các bội của 4.
Vậy trong các số đã cho, có 3 số là bội của 4.
Chọn đáp án C.
Câu 7:
Xem đáp án
Theo tính chất chia hết của một tổng: Ta có 49 chia hết cho 7 và 70 chia hết cho 7 nên 49 + 70 chia hết cho 7.
Chọn đáp án A.
Câu 8:
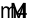và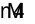 
thì m + n chia hết cho Xem đáp án
Vì 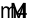và 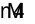nên theo tính chất chia hết của một tổng, ta có m + n chia hết cho 4.
Chọn đáp án A.
Câu 9:
Xem đáp án
Nhận thấy: 15 : 3 = 5 nên 15 chia hết cho 3 nên theo tính chất chia hết của một tích, ta có 15a luôn chia hết cho 3 với a là một số tự nhiên bất kì. Do đó đáp án B đúng.
Nếu ta lấy a = 1 thì 15a = 15 . 1 = 15 không chia hết cho 2, 4, 6 nên các đáp án A, C, D sai.
Chọn đáp án B.
Câu 10:
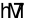và 
với h >k thì hiệu h – k chia hết cho: Xem đáp án
Theo tính chất chia hết của một hiệu, ta có
Với h >k, nếu 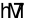và thì h – k chia hết cho 7.
Chọn đáp án A.