Đề thi Cuối kì học kỳ 2 Toán 6 có đáp án (Đề 1)
-
221 lượt thi
-
14 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Số đối của phân số \(\frac{4}{5}\) là \(\frac{{ - 4}}{5}\) vì \(\frac{{ - 4}}{5} + \frac{4}{5} = 0\).
Câu 2:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Quả dưa hấu đó nặng là \(0,8{\rm{ :}}\frac{{\rm{1}}}{3}{\rm{ = }}\frac{{\rm{4}}}{{\rm{5}}}{\rm{.}}\frac{3}{{\rm{1}}}{\rm{ = }}\frac{{{\rm{12}}}}{{\rm{5}}}{\rm{ = 2}}{\rm{,4 kg}}\).
Vậy quả dưa hấu đó nặng 2,4 kg.
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Vì: \(\frac{7}{{15}} + \frac{{ - 2}}{5} = \frac{7}{{15}} + \frac{{ - 6}}{{15}} = \frac{{7 + \left( { - 6} \right)}}{{15}} = \frac{1}{{15}}\)
Vậy tổng của hai phân số \(\frac{7}{{15}}\) và \(\frac{{ - 2}}{5}\) bằng \(\frac{1}{{15}}.\)
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Tổng số lần thực hiện hoạt động bắn mũi tên vào tấm bia là 20, số lần bắn trúng tấm bia là 18 lần.
Xác suất thực nghiệm bắn trúng bia là: \(\frac{{18}}{{20}} = \frac{9}{{10}}.\)
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Khi lấy ngẫu nhiên một viên bi, có 4 kết quả có thể xảy ra đối với màu của viên bi được lấy ra, đó là: màu vàng, màu trắng, màu đỏ, màu tím.
Câu 6:


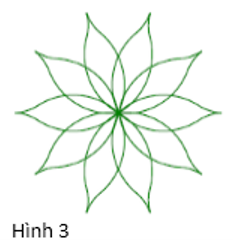
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Quan sát 3 hình trên a thấy cả ba hình đều có trục đối xứng và tâm đối xứng.
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°.
Câu 8:

 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Điểm B và D nằm khác phía so với điểm C.
Câu 9:
PHẦN II. TỰ LUẬN
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \[25\% - 1\frac{1}{4} + 0,2:\frac{6}{5}\];
b) \[\frac{8}{9} + \frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}\];
c) \(\frac{5}{{39}}\,\, \cdot \,\left( {\,7\frac{4}{5}\,\, \cdot \,1\frac{2}{3}\,\, + \,\,8\frac{1}{3}\, \cdot \,7\frac{4}{5}\,} \right)\)
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) \[25\% - 1\frac{1}{4} + 0,2:\frac{6}{5}\]
\[ = \frac{{25}}{{100}} - \frac{5}{4} + \frac{1}{5}:\frac{6}{5}\]
\[ = \frac{1}{4} - \frac{5}{4} + \frac{1}{5}.\frac{5}{6}\]
\[ = \left( {\frac{1}{4} - \frac{5}{4}} \right) + \frac{{1.5}}{{5.6}}\]
\[ = \frac{{ - 4}}{4} + \frac{1}{6}\]
\[ = - 1 + \frac{1}{6}\]
\[ = \frac{{ - 6}}{6} + \frac{1}{6}\]
\[ = \frac{{ - 5}}{6}\]
b) \[\frac{8}{9} + \frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}\]
\[ = \frac{8}{9} + \left( {\frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}} \right)\]
\[ = \frac{8}{9} + \frac{1}{9}.\left( {\frac{2}{9} + \frac{7}{9}} \right)\]
\[ = \frac{8}{9} + \frac{1}{9}.\frac{9}{9}\]
\[ = \frac{8}{9} + \frac{1}{9}.1\]
\( = \frac{8}{9} + \frac{1}{9}\)
\( = \frac{9}{9}\)
= 1.
c) \(\frac{5}{{39}}{\mkern 1mu} {\mkern 1mu} \, \cdot {\mkern 1mu} \,\left( {{\mkern 1mu} 7\frac{4}{5}\,{\mkern 1mu} {\mkern 1mu} \cdot \,1\frac{2}{3}{\mkern 1mu} {\mkern 1mu} \, + {\mkern 1mu} {\mkern 1mu} \,8\frac{1}{3}\,\, \cdot \,\,7\frac{4}{5}{\mkern 1mu} } \right)\)
\( = \,{\mkern 1mu} \frac{5}{{39}}{\mkern 1mu} {\mkern 1mu} \cdot \,{\mkern 1mu} \left[ {{\mkern 1mu} 7{\mkern 1mu} \frac{4}{5}\,{\mkern 1mu} \cdot \,{\mkern 1mu} \left( {1\frac{2}{3} + {\mkern 1mu} {\mkern 1mu} 8\frac{1}{3}{\mkern 1mu} } \right)} \right]\)
\( = \,{\mkern 1mu} \frac{5}{{39}}{\mkern 1mu} \, \cdot \,\frac{{39}}{5}{\mkern 1mu} \,\left( {1 + \frac{2}{3} + 8 + \frac{1}{3}} \right){\mkern 1mu} \)
\( = \,{\mkern 1mu} {\mkern 1mu} \frac{{5.39}}{{39.5}}{\mkern 1mu} {\mkern 1mu} \cdot\,{\mkern 1mu} \,\left( {9 + \frac{2}{3} + \frac{1}{3}} \right){\mkern 1mu} \)
\( = \,1{\mkern 1mu} \cdot\,\left( {9\, + \frac{3}{3}} \right){\mkern 1mu} \)
= 9 + 1
= 10.
Câu 10:
Tìm x biết:
a) ;
b) ;
c) 4x – (3 + 5x) = 14.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) \[\frac{{ - 5}}{{12}}:x = \frac{4}{{15}}\]
\[x = \frac{{ - 5}}{{12}}:\frac{4}{{15}}\]
\[x = \frac{{ - 5}}{{12}}.\frac{{15}}{4}\]
\(x = \frac{{ - 5.15}}{{12.4}}\)
\(x = \frac{{ - 5.3.5}}{{3.4.4}}\)
\[x = - \frac{{25}}{{16}}.\]
Vậy \[x = \frac{{ - 25}}{{16}}\].
b) \[\frac{3}{4}x - \frac{2}{3}x = \frac{2}{7}.\frac{1}{6} + \frac{5}{7}.\frac{1}{6}\]
\[\left( {\frac{3}{4} - \frac{2}{3}} \right)x = \frac{1}{6}.\frac{2}{7} + \frac{1}{6}.\frac{5}{7}\]
\[\left( {\frac{9}{{12}} - \frac{8}{{12}}} \right)x = \frac{1}{6}\left( {\frac{2}{7} + \frac{5}{7}} \right)\]
\(\frac{1}{{12}}.x = \frac{1}{6}.\frac{7}{7}\)
\[\frac{1}{{12}}x = \frac{1}{6}\]
\[x = \frac{1}{6}:\frac{1}{{12}}\]
\(x = \frac{1}{6}.\frac{{12}}{1}\)
x = 2.
Vậy x = 2.
c) 4x – (3 + 5x) = 14
4x – 3 – 5x = 14
4x – 5x = 14 + 3
(4 – 5).x = 17
–x = 17
x = –17.
Vậy x = –17.
Câu 11:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Số học sinh giỏi của lớp là: \(8:\frac{2}{3} = 12\) (học sinh)
Số học sinh khá của lớp là: 12 : 80% = 15 (học sinh)
Số học sinh trung bình của lớp là: \(\frac{7}{9}.(15 + 12) = 21\) (học sinh)
Số học sinh lớp \[6A\] là: 12 + 15 + 21 = 48 (học sinh).
Câu 12:
Trong một hộp kín có một số quả bóng màu xanh, màu đỏ, màu tím, vàng. Trong một trò chơi, người chơi được lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng. Minh thực hiện 100 lần và được kết quả sau:
|
Màu |
Số lần |
|
Xanh |
25 |
|
Đỏ |
23 |
|
Tím |
30 |
|
Vàng |
22 |
Hãy tìm xác suất của thực nghiệm của các sự kiện sau:
a) Minh lấy được quả bóng màu xanh;
b) Quả bóng được lấy ra không là màu đỏ.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) Quan sát bảng ta thấy bóng xanh được lấy 25 lần.
Xác suất của thực nghiệm sự kiện lấy được bóng xanh là: \(\frac{{25}}{{100}} = 0,25\)
b) Quan sát bảng ta thấy bóng đỏ được lấy ra 23 lần.
Do đó số lần Minh không lấy ra bóng đỏ là 100 – 23 = 77 (lần).
Xác suất của thực nghiệm sự kiện lấy ra không là màu đỏ là: \(\frac{{77}}{{100}} = 0,77\)
Câu 13:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:

Ta có C là điểm nằm giữa A và B nên AC + BC = AB.
Suy ra BC = AB – AB
Do đó BC = 8 – 3 = 5 cm. \(BC = AB - AC = 7 - 3 = 4cm\).
Vì M là trung điểm BC nên \(BM = \frac{{BC}}{2} = \frac{5}{2} = 2,5\) cm.
Câu 14:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có:
\(A = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}}\)
\( = \frac{1}{{{2^2}}}\left( {1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}}} \right)\).
Mặt khác ta có: \(\frac{1}{{{2^2}}} = \frac{1}{{2.2}} < \frac{1}{{1.2}} = \frac{{2 - 1}}{{1.2}} = \frac{2}{{1.2}} - \frac{1}{{1.2}} = 1 - \frac{1}{2}\)
\(\frac{1}{{{3^2}}} = \frac{1}{{3.3}} < \frac{1}{{2.3}} = \frac{{3 - 2}}{{2.3}} = \frac{3}{{2.3}} - \frac{2}{{2.3}} = \frac{1}{2} - \frac{1}{3}\)
………………..
\(\frac{1}{{{{50}^2}}} = \frac{1}{{50.50}} < \frac{1}{{49.50}} = \frac{{50 - 49}}{{49.50}} = \frac{{50}}{{49.50}} - \frac{{49}}{{49.50}} = \frac{1}{{49}} - \frac{1}{{50}}\)
Do đó \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}} < 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{49}} - \frac{1}{{50}}\)
Suy ra \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}} < 1 - \frac{1}{{50}}\)
\(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}} < \frac{{49}}{{50}} < \frac{{50}}{{50}} = 1\)
\(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}} < 1\)
Từ đó ta có: \(1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}} < 1 + 1 = 2\)
\[A = \frac{1}{{{2^2}}}\left( {1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{50}^2}}}} \right) < \frac{1}{4}.2 = \frac{1}{2}\].
Vậy \(A < \frac{1}{2}.\)
