Đề kiểm tra Giữa kì 2 Toán 8 CD có đáp án (Đề 2)
-
121 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Một trường THCS phát động phong trào biểu diễn văn nghệ nhân ngày nhà giáo Việt Nam 20/11 cho học sinh tất cả các lớp. Biết rằng mỗi lớp chỉ biểu diễn tối đa 3 tiết mục. Bảng thống kê số tiết mục đăng kí tham gia diễn văn nghệ của từng lớp như bảng dưới đây:
|
Lớp |
6A |
6B |
7A |
7B |
8A |
8B |
9A |
9B |
|
Số tiết mục |
2 |
3 |
5 |
3 |
2 |
2 |
3 |
2 |
Theo em, số liệu của lớp nào trong bản trên là không hợp lí?
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 3:
Thành phần của một loại thép được biểu diễn trong biểu đồ dưới đây:
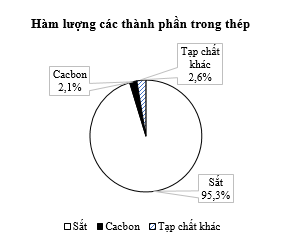
Khối lượng sắt trong một thanh thép nặng 1 kg là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 4:
Gieo 90 lần một con xúc xắc cân đối và đồng chất ta được kết quả như sau:
|
Mặt |
|
|
|
|
|
|
|
Số lần xuất hiện |
18 |
12 |
14 |
26 |
12 |
8 |
Xác suất thực nghiệm của sự kiện gieo được mặt có số chấm nhỏ hơn 3 là:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 5:
Cho tam giác ABC, AD là đường phân giác của Tỉ lệ thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 8:
Cho tam giác ABC có D, E lần lượt là trung điểm của các cạnh AB, AC và DE = 4 cm Biết đường cao AH = 6 cm, diện tích tam giác ABC là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 9:
Thống kê tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định từ tháng 1 đến tháng 12 lần lượt là: (đơn vị: giờ) (Nguồn: Tổng cục thống kê).
a) Lập bảng số liệu thống kê theo mẫu dưới đây và vẽ biểu đồ phù hợp để biểu diễn tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Tổng số giờ nắng (h) |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
? |
b) Tổng số giờ nắng tại trạm quan trắc Nam Định trong tháng nào cao nhất? Thấp nhất?
c) Một bài báo có nêu thông tin: “So với tháng 9, tổng số giờ nắng tại trạm quan trắc Nam Định trong tháng 10 tăng lên xấp xỉ 34%”. Thông tin của bài báo đó có chính xác không?
 Xem đáp án
Xem đáp án
a) Ta lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 như sau:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Tổng số giờ nắng (h) |
34,4 | 27,5 | 49,4 | 108,2 | 88,8 | 186,6 | 190,7 | 151,7 | 133,2 | 165,0 | 126,2 | 102,1 |
Ta vẽ biểu đồ đoạn thẳng biểu diễn số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định như sau:
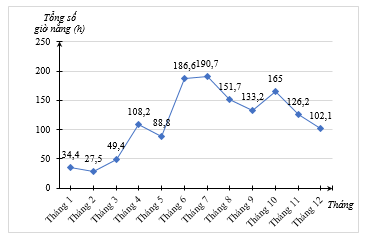
b) Số giờ nắng tại Nam Định trong tháng 7 là cao nhất (190,7 h) và tháng 2 là thấp nhất (27,5 h).
c) So với tháng 9, số giờ nắng tại Nam Định trong tháng 10 bằng
Khi đó tháng 10 tăng khoảng so với tháng 9.
Vậy thông tin của bài báo đó không chính xác.
Câu 10:
Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau:
|
Số khách |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Số ngày |
3 |
6 |
5 |
9 |
3 |
2 |
1 |
1 |
a) Gọi A là biến cố “Trong một ngày có từ 3 khách trở lên đến cơ quan”. Hỏi có bao nhiêu ngày biến cố A xảy ra?
b) Tính xác suất thực nghiệm của biến cố A.
c) Hãy ước lượng xác suất của biến cố B: “Trong một ngày có số khách đến cơ quan là số lẻ”.
 Xem đáp án
Xem đáp án
a) Theo bảng thống kê, số ngày có từ 3 khách trở lên đến cơ quan là:
(ngày).
b) Số ngày bác bảo vệ theo dõi là: (ngày).
Xác suất thực nghiệm của biến cố A là:
c) Theo bảng thống kê, số ngày có khách đến cơ quan là số lẻ là (ngày)
Xác suất thực nghiệm của biến cố B là
Vậy xác suất của biến cố B được ước lượng là 60%
Câu 11:
Cho Tia phân giác góc trong của góc A cắt BC tại D Cho AB = 6, AC = x, BD = 9, BC = 21. Tìm x.
 Xem đáp án
Xem đáp án
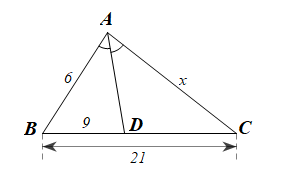
Ta có: nên
Trong AD là phân giác của nên (tính chất đường phân giác của tam giác)Hay , suy ra
Câu 12:
Cho tam giác ABC, các đường trung tuyến BD, CE Gọi M, N theo thứ tự là trung điểm của BE, CD Gọi I, K theo thứ tự là giao điểm của MN với BD và CE Chứng minh rằng:
a) ED // BC b) MN // BC c) MI = IK = KN.
 Xem đáp án
Xem đáp án
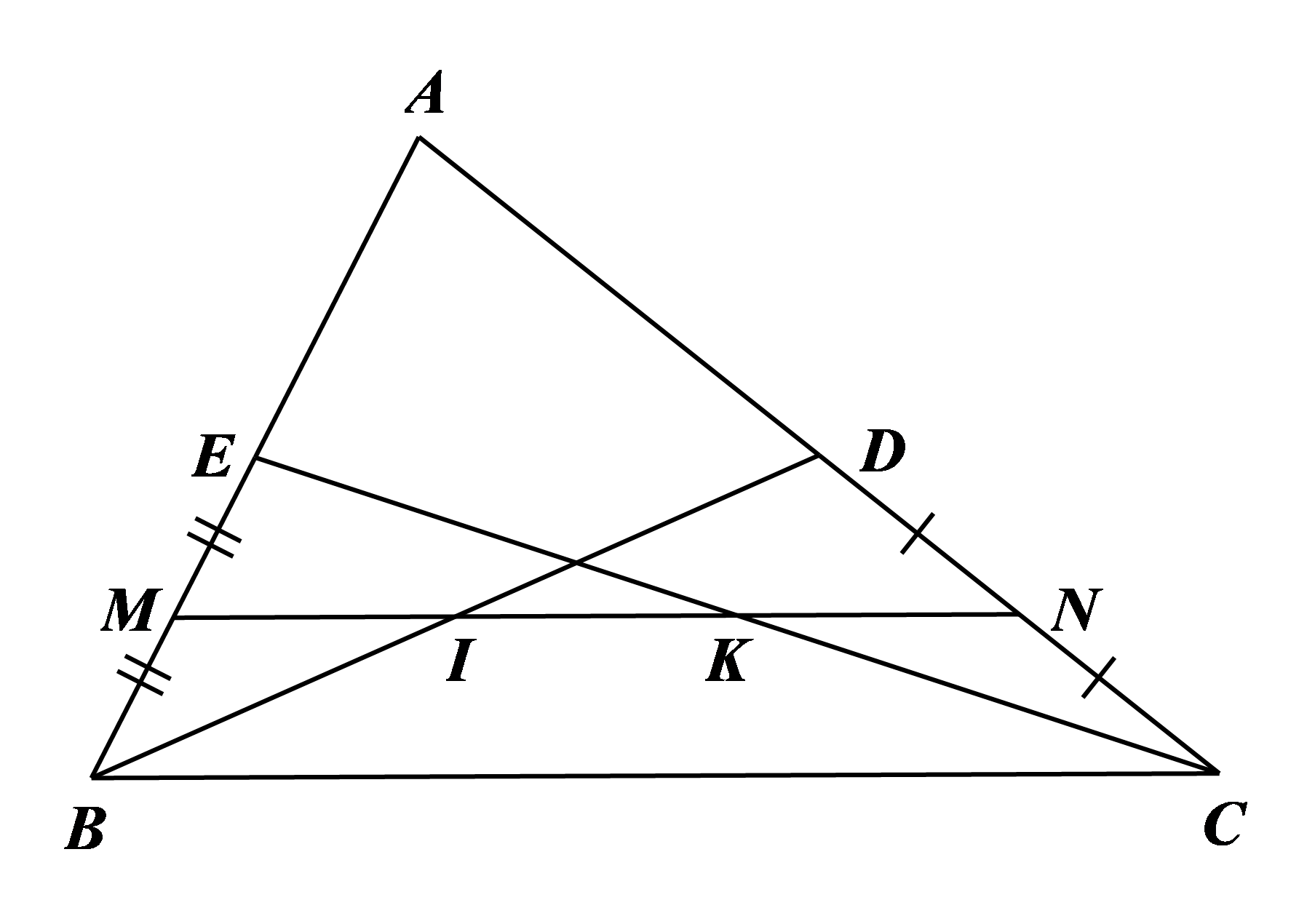
a) Trong có các đường trung tuyến BD, CE nên D là trung điểm của AC, E là trung điểm của AB nên ED là đường trung bình của
Suy ra và (tính chất đường trung bình của tam giác).b) Ta có: E là trung điểm của AB nên
Mà M là trung điểm của EB nên hay
Tương tự, ta cũng có hay
Suy ra
Xét có nên (định lí Thalès đảo).
c) Ta có (câu b) và (câu a) nên
Xét có M là trung điểm của EB và (do
Suy ra I là trung điểm của BD hay IB = ID
Khi đó MI là đường trung bình của nên
Tương tự, trong DCDE ta cũng có trong DBCE có
Ta có .
Do đó .