Giải SGK Toán 8 (Cánh Diều) Bài 1: Hàm số

Giải bài tập Toán lớp 8 Bài 1: Hàm số

Video bài giải Toán lớp 8 Bài 1: Hàm số - Cánh diều

Khởi động trang 55 Toán 8 Tập 1: Thanh long là một loại cây chịu hạn, rất thích hợp với điều kiện khí hậu và thổ nhưỡng của tỉnh Bình Thuận. Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng. Với mỗi lượng thanh long loại I được bán ra, người bán sẽ thu được một số tiền tương ứng.

Mối liên quan giữa hai đại lượng số kilôgam thanh long được bán ra và số tiền người bán thu được thể hiện khái niệm nào trong toán học?

Lời giải:

Sau khi học xong bài này ta sẽ giải quyết bài toán này như sau:

Ta tính số tiền người bán thu được bằng công thức:

Số tiền người bán thu được = giá bán 1 kg × số kilôgam thanh long được bán ra 

Hay: Số tiền người bán thu được = 32 000 × số kilôgam thanh long được bán ra

Khi đó, ta thấy số tiền người bán thu được phụ thuộc vào số kilôgam thanh long được bán ra (với số kilôgam thanh long được bán ra khác nhau thì số tiền người bán thu được khác nhau).

Do đó, số tiền người bán thu được gọi là hàm số của số kilôgam thanh long được bán ra.

I. Định nghĩa

Hoạt động 1 trang 55 Toán 8 Tập 1: Chu vi y (cm) của hình vuông có độ dài cạnh x (cm) được tính theo công thức y = 4x. Với mỗi giá trị của x, xác định được bao nhiêu giá trị tương ứng của y?

Lời giải:

Chu vi y (cm) của hình vuông có độ dài cạnh x (cm) đều là các giá trị dương. Với mỗi giá trị của x, ta xác định được một giá trị tương ứng của y.

Thay các giá trị của x vào công thức tính chu vi ta tìm giá trị các giá trị tương ứng của y.

Chẳng hạn:

• Với x = 1 cm, ta có: y = 4x = 4 . 1 = 4 (cm);

• Với $x=\frac{2}{7}$ cm, ta có: $y=4.\frac{2}{7}=\frac{8}{7}$ (cm);

• Với x = 3,2 cm, ta có: y = 4 . 3,2 = 12,8 (cm);

...

Hoạt động 2 trang 55 Toán 8 Tập 1: Trong tình huống ở phần mở đầu, hãy cho biết:

a) Số tiền người bán thu được khi lần lượt bán 2 kg thanh long; 3 kg thanh long.

b) Gọi y (đồng) là số tiền người bán thu được khi bán x (kg) thanh long. Với mỗi giá trị của x, ta xác định được bao nhiêu giá trị tương ứng của y?

Lời giải:

a) Giá bán 1 kg thanh long ruột đỏ loại I là 32 000 đồng.

Số tiền người bán thu được khi bán 2 kg thanh long là:

32 000 . 2 = 64 000 (đồng).

Số tiền người bán thu được khi bán 3 kg thanh long là:

32 000 . 3 = 96 000 (đồng).

Vậy số tiền người bán thu được khi lần lượt bán 2 kg thanh long; 3 kg thanh long lần lượt là 64 000 đồng; 96 000 đồng.

b) Với mỗi giá trị của x, ta xác định được một giá trị tương ứng của y.

Luyện tập 1 trang 56 Toán 8 Tập 1: Cho hai ví dụ về hàm số.

Lời giải:

Có nhiều ví dụ về hàm số. Chẳng hạn:

Hai ví dụ về hàm số: $y=4x;y=\frac{1}{3}x$.

II. Giá trị của hàm số

Hoạt động 3 trang 57 Toán 8 Tập 1: : Một xe ô tô chạy với tốc độ 60 km/h trong thời gian t (h).

a) Viết hàm số biểu thị quãng đường S(t) (km) mà ô tô đi được trong thời gian t(h).

b) Tính quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 2 (h); t = 3 (h).

Lời giải:

a) Xe ô tô chạy với tốc độ 60 km/h hay vận tốc của ô tô là 60 km/h.

Hàm số biểu thị quãng đường S(t) (km) mà ô tô đi được trong thời gian t(h) là: S(t) = 60t (km).

b) Quãng đường S(t) (km) mà ô tô đi được trong thời gian t = 2 (h); t = 3 (h) lần lượt là:

• Với t = 2 (h), ta có S(2) = 60 . 2 = 120 (km);

• Với t = 3 (h), ta có S(3) = 60 . 3 = 180 (km).

Luyện tập 2 trang 57 Toán 8 Tập 1: Cho hàm số f(x) = −5x + 3.

Tính $f\left(0\right);f(-1);f\left(\frac{1}{2}\right).$

Lời giải:

Thay lần lượt các giá trị x = 0; x = −1; $x=\frac{1}{2}$ vào hàm số f(x), ta được:

• f(0) = −5 . 0 + 3 = 0 + 3 = 3;

• f(−1) = (−5) . (−1) + 3 = 5 + 3 = 8;

• $f\left(\frac{1}{2}\right)=-5.\frac{1}{2}+3=\frac{-5}{2}+3=\frac{1}{2}$.

Vậy f(0) = 3; f(−1) = 8; $f\left(\frac{1}{2}\right)=\frac{1}{2}$.

Bài tập

Bài 1 trang 58 Toán 8 Tập 1: Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng được cho bởi mỗi trường hợp sau:

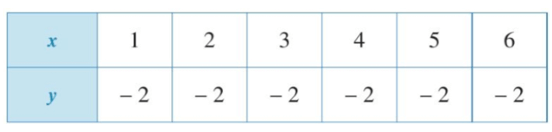
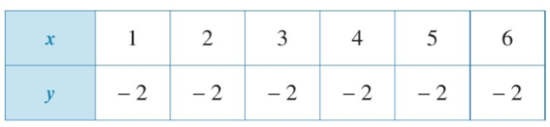
a)

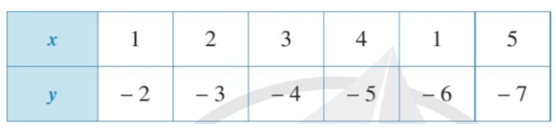
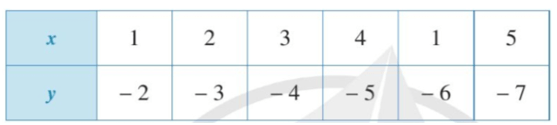
b)

Lời giải:

a)

Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 5; x = 6 thì ta đều xác định  giá trị của y là y = − 2.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

b)

Quan sát bảng trên ta thấy khi x = 1; x = 2; x = 3; x = 4; x = 1; x = 5 thì ta đều xác định  giá trị của y lần lượt là: y = − 2; y = − 3; y = − 4; y = − 5; y = − 6; y = − 7.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

Bài 2 trang 58 Toán 8 Tập 1: a) Cho hàm số y = 2x + 10. Tìm giá trị của y tương ứng với mỗi giá trị sau của x:

$x=-5;x=0;x=\frac{1}{2}.$

b) Cho hàm số f(x) = −2x² + 1. Tính $f(-1);f\left(0\right);f\left(\frac{1}{3}\right).$

Lời giải:

a) Thay lần lượt các giá trị $x=-5;x=0;x=\frac{1}{2}$ vào hàm số y = 2x + 10.

• Với x = − 5, ta có: y = 2 . (− 5) + 10 = − 10 + 10 = 0;

• Với x = 0, ta có: y = 2 . 0 + 10 = 0 + 10 = 10;

• Với $x=\frac{1}{2}$, ta có: $y=2.\frac{1}{2}+10=1+10=11$.

Vậy với $x=\frac{1}{2}$ ta xác định được giá trị tương ứng của y lần lượt là y = 0; y = 10; y = 11.

b) Thay lần lượt các giá trị $x=-1;x=0;x=\frac{1}{3}$ vào hàm số f(x) = −2x² + 1.

• f(− 1) = − 2 . (− 1)² + 1 = − 2 . 1 + 1 = − 2  + 1 = − 1;

• f(0) = − 2 . 0² + 1 = 0 + 1 = 1;

• $f\left(\frac{1}{3}\right)=-2.{\left(\frac{1}{3}\right)}^2+1=-2.\frac{1}{9}+1=\frac{-2}{9}+1=\frac{7}{9}$.

Vậy $f(-1)=-1;f\left(0\right)=1;f\left(\frac{1}{3}\right)=\frac{7}{9}$.

Bài 3 trang 58 Toán 8 Tập 1: Cho một thanh kim loại đồng chất có khối lượng riêng là 7,8 g/cm³.

a) Viết công thức tính khối lượng m (g) theo thể tích V (cm³). Hỏi m có phải là hàm số của V hay không? Vì sao?

b) Tính khối lượng của thanh kim loại đó khi biết thể tích của thanh kim loại đó là

V = 1 000 cm³.

Lời giải:

a) Công thức tính khối lượng m (g) theo thể tích V (cm³) là: V = 7,8m.

Suy ra $m=\frac{V}{\mathrm{7,8}}$.

Với mỗi giá trị của V ta xác định được một giá trị của m nên m là hàm số của V.

b) Với V = 1 000 cm³ ta có $m=\frac{1000}{\mathrm{7,8}}=\frac{5000}{39}$ (g).

Vậy khi biết thể tích của thanh kim loại đó là V = 1 000 cm³ thì khối lượng của thanh kim loại đó là $\frac{5000}{39}$ g.

Bài 4 trang 58 Toán 8 Tập 1: Dừa sáp là một trong những đặc sản lạ, quý hiếm và có giá trị dinh dưỡng cao, thường được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp. Hỏi y có phải là hàm số của x hay không? Vì sao?

b) Hãy tính số tiền mà người mua phải trả khi mua 10 quả dừa sáp.

Lời giải:

Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp là

y = 200 000x (đồng) .

Vì với mỗi giá trị của x ta xác định được một giá trị y tương ứng nên y là hàm số của x.

b) Số tiền mà người mua phải trả khi mua 10 quả dừa sáp là:

200 000 . 10 = 2 000 000 (đồng).

Vậy số tiền mà người mua phải trả khi mua 10 quả dừa sáp là 2 000 000 đồng.

Bài 5 trang 59 Toán 8 Tập 1: Bác Ninh gửi tiết kiệm 10 triệu đồng ở ngân hàng với kì hạn 12 tháng và không rút tiền trước kì hạn. Lãi suất ngân hàng quy định cho kì hạn 12 tháng là r%/năm.

a) Viết công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng. Hỏi y có phải là hàm số của r hay không? Vì sao?

b) Tính số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng, biết r = 5,6.

Lời giải:

a) Công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng là: y = 10r% (triệu đồng).

Vì với mỗi giá trị của r thì ta xác định được một giá trị tương ứng của y nên y là hàm số của r.

b) Với r = 5,6 thì số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng là:

y = 10r% = 10 . 5,6% = 0,56 (triệu đồng) = 560 000 (đồng).

Vậy với r = 5,6 thì số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng là 560 000 đồng.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Hoạt động thực hành và trải nghiệm Chủ đề 1: Quản lí tài chính cá nhân

Chủ đề 1: Quản lí tài chính cá nhân

Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)