Giải SGK Toán 6 Bài 1 (Cánh diều): Tam giác đều. Hình vuông. Lục giác đều

Giải Toán lớp 6 Bài 1: Tam giác đều. Hình vuông. Lục giác đều

Giải Toán 6 trang 93 Tập 1

Toán lớp 6 trang 93 Hoạt động 1: Hãy sắp xếp ba chiếc que có độ dài bằng nhau để tạo thành tam giác như Hình 1. Tam giác đó được gọi là tam giác đều.

Lời giải:

Em sử dụng ba que diêm hoặc ba que tính bằng nhau để xếp theo Hình 1.

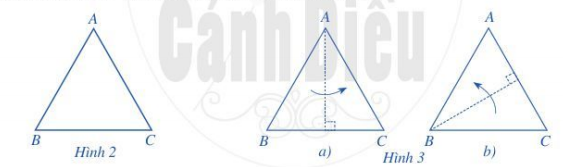
Toán lớp 6 trang 93 Hoạt động 2: Với tam giác đều ABC như ở Hình 2, thực hiện hoạt động sau:

a) Gấp tam giác ABC sao cho cạnh AB trùng với cạnh AC, đỉnh B trùng với đỉnh C (Hình 3a). So sánh cạnh AB và cạnh AC; góc ABC và góc ACB. 

b) Gấp tam giác ABC sao cho cạnh BC trùng với cạnh BA, đỉnh C trùng với đỉnh A (Hình 3b). So sánh cạnh BC và cạnh BA; góc BCA và góc BAC. 

Lời giải:

a) Sau khi gấp hình ta thấy cạnh AB trùng với cạnh AC nên AB = AC

Khi đó góc ACB cung trùng với góc ACB nên hai góc này bằng nhau.

b) Tương tự câu a, ta có BC = BA và hai góc BCA và BAC bằng nhau.

Giải Toán 6 trang 94 Tập 1

Toán lớp 6 trang 94 Hoạt động 3: Vẽ tam giác đều bằng thước và compa khi biết độ dài cạnh.

Lời giải:

Ví dụ: Ta dùng thước và compa vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm.

Để vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm, ta làm như sau:

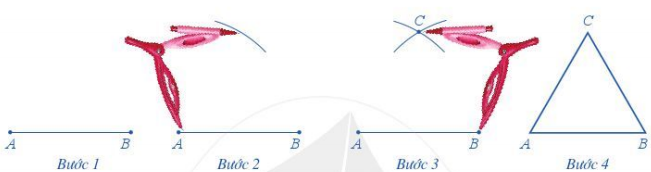
Bước 1. Dùng thước vẽ đoạn thẳng AB = 3 cm

Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.

Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.

Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC.

Vậy ta được tam giác đều ABC có cạnh bằng 3 cm.

Toán lớp 6 trang 94 Luyện tập 1: Hãy dùng thước và compa vẽ tam giác đều EGH có độ dài cạnh bằng 4 cm.

Lời giải:

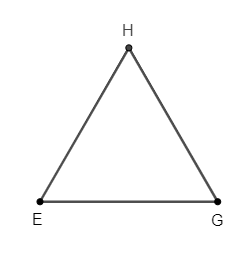
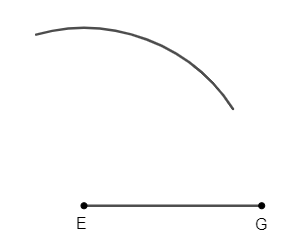
Để vẽ tam giác đều EGH có độ dài cạnh bằng 4 cm, ta làm như sau:

Bước 3

Bước 4

 Bước 1. Dùng thước vẽ đoạn thẳng EG = 4 cm

Bước 2. Lấy E làm tâm, dùng compa vẽ một phần đường tròn có bán kính EG.

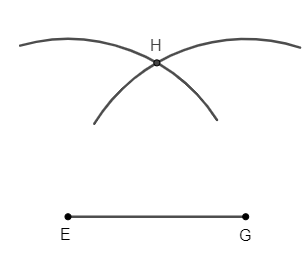
Bước 3. Lấy G làm tâm, dùng compa vẽ một phần đường tròn có bán kính GE; gọi H là giao điểm của hai phần đường tròn vừa vẽ.

Bước 4. Dùng thước vẽ các đoạn thẳng EH và GH.

Khi đó ta được tam giác đều EGH có độ dài cạnh bằng 4 cm.

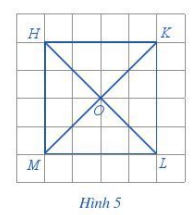
Toán lớp 6 trang 94 Hoạt động 4: Với hình vuông HKLM ở Hình 5, thực hiện hoạt động sau:

a) Đếm số ô vuông để so sánh độ dài các cạnh HK, KL, LM, MH.

b) Quan sát xem các cạnh đối HK và ML; HM và KL của hình vuông HKLM có song song với nhau không.

c) Đếm số ô vuông để so sánh độ dài hai đường chéo KM và HL.

d) Nêu đặc điểm bốn góc ở các đỉnh H, K, L, M.

Lời giải:

Quan sát Hình 5 ta thấy:

a) Độ dài các cạnh HK, KL, LM, MH bằng nhau và đều bằng 4 ô vuông.

b) Các cạnh đối HK và ML, HM và KL của hình vuông HKLM song song với nhau.

c) Độ dài đường chéo KM và HL bằng nhau và đều bằng 4 phần đường chéo của ô vuông nhỏ.

d) Bốn góc ở các đỉnh H, K, L, M là các góc vuông.

Giải Toán 6 trang 95 Tập 1

Toán lớp 6 trang 95 Hoạt động 5: Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh.

Lời giải:

Ví dụ: Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng 7 cm.

Để vẽ hình vuông ABCD, ta làm như sau:

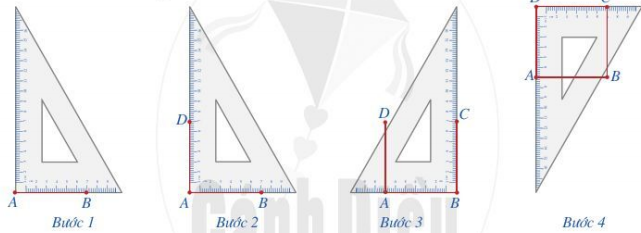
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 7cm.

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 7cm.

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 7cm.

Bước 4. Vẽ đoạn thẳng CD.

Vậy ta được hình vuông ABCD có cạnh bằng 7 cm.

Toán lớp 6 trang 95 Luyện tập 2: Vẽ bằng ê ke hình vuông EGHI có độ dài cạnh bằng 6 cm.

Lời giải:

Để vẽ hình vuông EGHI, ta làm như sau:

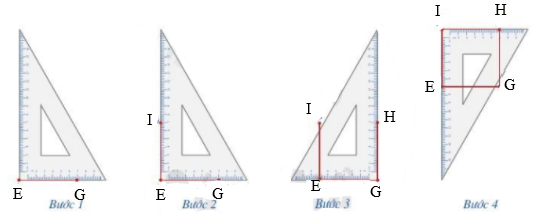
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng EG có độ dài bằng 6 cm.

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm E và một cạnh ê ke nằm trên EG, vẽ theo cạnh kia của ê ke đoạn thẳng EI có độ dài bằng 6 cm.

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh GH có độ dài bằng 6 cm.

Bước 4. Vẽ đoạn thẳng HI.

Khi đó ta được hình vuông EGHI có độ dài cạnh bằng 6 cm.

Giải Toán 6 trang 96 Tập 1

Toán lớp 6 trang 96 Hoạt động 6:

a) Hãy ghép sáu miếng phẳng hình tam giác đều có cạnh bằng nhau để tạo thành hình lục giác như ở Hình 7. Hình lục giác đó gọi là hình lục giác đều.

b) Vẽ đường viền xung quanh sáu cạnh của hình lục giác đều ở Hình 7 ta được lục giác đều và đặt tên các đỉnh của lục giác đều đó.

Lời giải:

a)

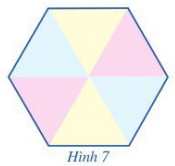
Chuẩn bị 6 miếng bìa hình tam giác đều bằng nhau và ghép lại như Hình 7.

b) Ta được hình lục giác đều ABCDEF.

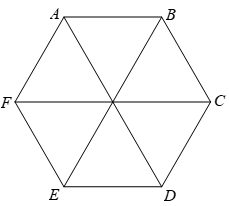
Toán lớp 6 trang 96 Hoạt động 7: Quan sát lục giác đều ABCDEG ở Hình 8.

Lời giải:

Quan sát lục giác đều ABCDEG ở Hình 8 ta thấy:

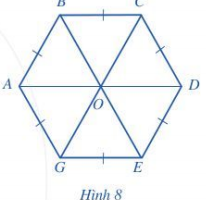
a) Các tam giác OAB, OBC, OCD, ODE, OEG, OGA là tam giác đều nên các cạnh AB, BC, CD, DE, EG, GA có độ dài bằng nhau.

b) Các đường chéo chính AD, BE, CG cắt nhau tại điểm O.

c) Các đường chéo chính AD, BE, CG có độ dài gấp đôi độ dài cạnh tam giác đều nên chúng bằng nhau.

d) Mỗi góc ở đỉnh A, B, C, D, E, G của lục giác đều ABCDEG đều gấp đôi góc của một tam giác đều nên chúng bằng nhau.

Bài tập

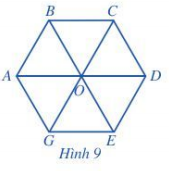
Toán lớp 6 trang 96 Bài 1: Cho lục giác đều ABCDEG.

Các đường chéo chính AD, BE, CG, cắt nhau tại O (Hình 9).

Vì sao OA = OB = OC = OD = OE = OG?

Lời giải:

Vì ABCDEG là lục giác đều nên:

Các đường chéo chính AD, BE, CG bằng nhau và cắt nhau tạo O, tạo nên các tam giác đều ABO, BCO, CDO, DOE, GOE, AGO

Lại có trong tam giác đều, ta có ba cạnh bằng nhau, nên

AB = OB = OA

BC = OB = OC

CD = OD = OC

OD = OE = DE

OG = OE = GE

AG = OG = OA

Do đó:  OA = OB = OC = OD = OE = OG.

Giải Toán 6 trang 97 Tập 1

Toán lớp 6 trang 97 Bài 2: Một mảnh vườn có dạng hình vuông với chiều dài cạnh bằng 25m. Người ta để một phần của mảnh vườn làm lối đi rộng 2m như Hình 10, phần còn lại để trồng rau.

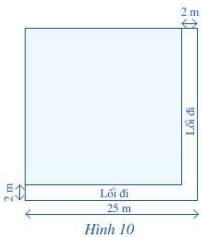
a) Tính diện tích phần vườn trồng rau.

b) Người ta làm hàng rào xung quanh mảnh vườn trồng rau và ở một góc vườn rau có để cửa ra vào rộng 2m. Tính độ dài của hàng rào đó.

Lời giải:

a) Vì người ta để một phần của mảnh vườn làm lối đi rộng 2 m nên phần vườn trồng rau là mảnh đất hình vuông và có độ dài cạnh là:

25 – 2 = 23 (m)

Diện tích phần vườn trồng rau là:

23 . 23 = 529 (m²)

b) Chu vi của phần vườn trồng rau hình vuông là:

4 . 23 = 92 (m)

Độ dài của hàng rào chính là chu vi của phần vườn trồng rau trừ đi phần cửa ra vào rộng 2 m. Do đó độ dài của hàng rào là:

92 – 2 = 90 (m)

Vậy diện tích của phần vườn trồng rau là 529 m², độ dài của hàng rào là 90 m.

Toán lớp 6 trang 97 Bài 3: Hướng dẫn cách gấp và cắt giấy hình tam giác đều, hình lục giác đều từ một hình vuông

a) Gấp giấy theo thứ tự trong Hình 11 từ a) đến c), sau đó cắt theo viền đỏ như Hình 11c, ta sẽ được một hình tam giác đều.

b) Gấp giấy theo thứ tự trong Hình 12 từ a) đến g), sau đó cắt theo viền đỏ như Hình 12g, ta sẽ được một hình lục giác đều.

Lời giải:

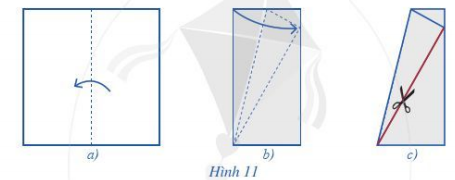
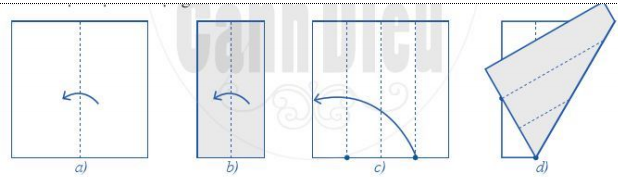
Học sinh cắt một mảnh giấy hình vuông và thực hiện theo các bước trong Hình 11 và Hình 12 để có được tam giác đều và lục giác đều.

Toán lớp 6 trang 97 Bài 4: 

Đố vui: Đố bạn chỉ với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau) mà xếp được thành 6 tam giác đều.

Lời giải:

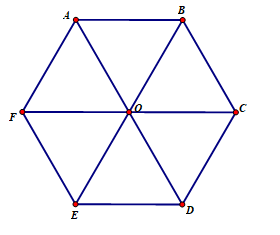
Với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau), ta có thể xếp chúng thành hình lục giác đều với các đường chéo chính cắt nhau như hình trên, ta được 6 hình tam giác đều.

Xem thêm lời giải SGK Toán lớp 6 sách Cánh diều hay, chi tiết khác:

Bài 6: Phép chia hết hai số nguyên. Quan hệ chia hết trong tập hợp số nguyên

Bài tập cuối chương 2

Bài 2: Hình chữ nhật, hình thoi

Bài 3: Hình bình hành

Bài 4: Hình thang cân