Giải SBT Toán 7 (Chân trời sáng tạo) Bài 1: Các góc ở vị trí đặc biệt

Giải Sách bài tập Toán lớp 7 Bài 1: Các góc ở vị trí đặc biệt

Giải SBT Toán 7 trang 75 Tập 1

Bài 1 trang 75 Sách bài tập Toán 7 Tập 1: Cho Hình 11.

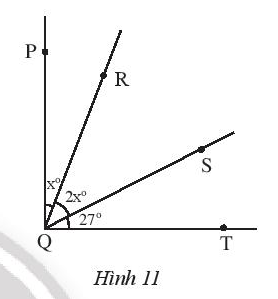
a) Tìm các góc kề với $\widehat{RQS}.$

b) Cho biết $\widehat{PQT}=90°.$ Tìm số đo của các góc $\widehat{RQS}$ và $\widehat{RQP}.$

Lời giải

a) Các góc kề với $\widehat{RQS}$ là: $\widehat{PQR}$ và $\widehat{SQT}.$

b) Vì $\widehat{RQS}$ kề với $\widehat{PQR}$ và $\widehat{SQT}$ nên ta có:

$\widehat{PQR}+\widehat{RQS}+\widehat{SQT}=\widehat{PQT}$

Hay x° + 2x° + 27° = 90°

Suy ra 3x° = 63°

Do đó x° = 21°.

Suy ra 2x° = 2.21° = 42°.

Vậy $\widehat{RQS}=2x°=42°$ và $\widehat{RQP}=x°=21°.$

Bài 2 trang 75 Sách bài tập Toán 7 Tập 1: Tìm số đo góc có dấu “?” trong Hình 12.

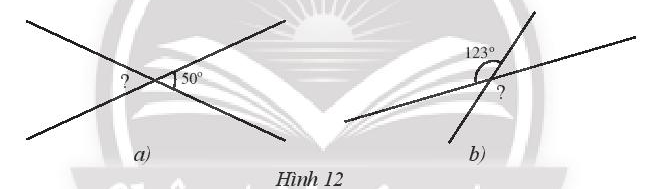
Lời giải

a)

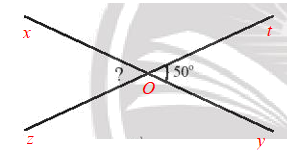
Giả sử đường thẳng xy cắt zt tạo điểm O tạo thành $\widehat{tOy}=50°$ như hình vẽ.

Ta cần đi tìm số đo của góc xOz.

Ta có: $\widehat{xOz}$ và $\widehat{tOy}$ là hai góc đối đỉnh.

Nên $\widehat{xOz}=\widehat{tOy}=50°.$

Vậy $\widehat{xOz}=50°.$

b)

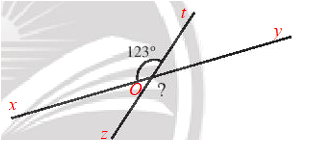
Giả sử đường thẳng xy cắt zt tạo điểm O tạo thành $\widehat{xOt}=123°$ như hình vẽ.

Ta cần đi tìm số đo của góc zOy.

Ta có: $\widehat{xOt}$ và $\widehat{zOy}$ là hai góc đối đỉnh.

Nên $\widehat{zOy}=\widehat{xOt}=123°.$

Vậy $\widehat{zOy}=123°.$

Bài 3 trang 75 Sách bài tập Toán 7 Tập 1: Tìm số đo các góc chưa biết trong Hình 13.

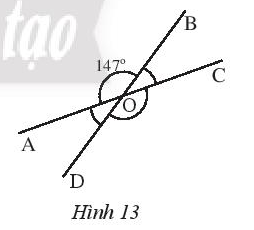
Lời giải

• Ta có: $\widehat{AOB}$ và $\widehat{COD}$ là hai góc đối đỉnh nên:

$\widehat{COD}=\widehat{AOB}=147°.$

• Vì $\widehat{AOB}$ và $\widehat{BOC}$ là hai góc kề bù nên:

$\widehat{AOB}+\widehat{BOC}=180°$

Suy ra $\widehat{BOC}=180°-\widehat{AOB}=180°-147°=33°.$

• Ta lại có: $\widehat{BOC}$ và $\widehat{AOD}$ là hai góc đối đỉnh nên:

$\widehat{AOD}=\widehat{BOC}=33°.$

Vậy $\widehat{BOC}=33°,\widehat{COD}=147°$ và $\widehat{AOD}=33°.$

Bài 4 trang 75 Sách bài tập Toán 7 Tập 1: Tìm giá trị của x trong Hình 14.

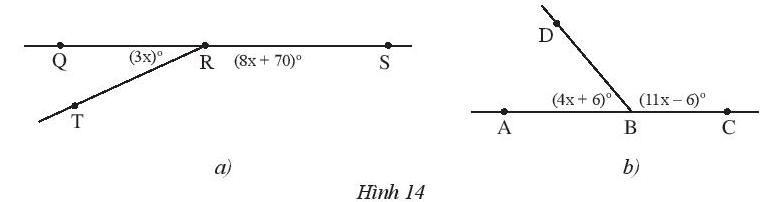
Lời giải

a) Vì $\widehat{QRT}$ và $\widehat{TRS}$ là hai góc kề bù nên:

$\widehat{QRT}+\widehat{TRS}=180°$

Suy ra (3x)° + (8x + 70)° = 180°

Nên (3x + 8x + 70)° = 180°

Do đó 11x + 70 = 180

Suy ra 11x = 110

Suy ra x = 10.

Vậy x = 10.

b) Vì $\widehat{ABD}$ và $\widehat{DBC}$ là hai góc kề bù nên:

$\widehat{ABD}+\widehat{DBC}=180°$

Suy ra (4x + 6)° + (11x – 6)° = 180°

Nên (4x + 6 + 11x – 6)° = 180°

Do đó 15x = 180

Suy ra x = 12.

Vậy x = 12.

Giải SBT Toán 7 trang 76 Tập 1

Bài 5 trang 76 Sách bài tập Toán 7 Tập 1: Cho Hình 15 chứng minh hai đường thẳng xy và zt vuông góc.

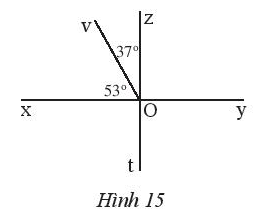
Lời giải

Vì $\widehat{xOv}$ và $\widehat{vOz}$ là hai góc kề nhau nên:

$\widehat{xOv}+\widehat{vOz}=\widehat{xOz}$

Do đó $\widehat{xOz}=53°+37°=90°$

Suy ra Ox ⊥ Oz hay xy ⊥ zt.

Vậy hai đường thẳng xy và zt vuông góc.

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

Bài tập cuối chương 3

Bài 2: Tia phân giác

Bài 3: Hai đường thẳng song song

Bài 4: Định lí và chứng minh một định lí