Sách bài tập Toán 6 Bài tập cuối chương 6
Bài 1 trang 61 sách bài tập Toán lớp 6 Tập 2: Hãy sắp xếp các số thập phân sau theo thứ tự giảm dần:
−5,24; 0,6; 1,41; 5,4; 0,22; −4,125; −0,26.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự giảm dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập phân dương và số thập phân âm, vì số thập phân dương luôn lớn hơn số thập phân âm.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:
* Phân loại:
- Nhóm các số thập phân dương: 0,6; 1,41; 5,4; 0,22.
- Nhóm các số thập phân âm: −5,24; −4,125; −0,26.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương:
+ Phần nguyên của số 0,6 và 0,22 là 0; ta so sánh hàng phần mười của hai số. Vì 6 > 2 nên 0,6 > 0,22.
+ Phần nguyên của số 1,41 là 1;
+ Phần nguyên của số 5,4 là 5.
Do đó 5,4 > 1,41 > 0,6 > 0,22 (các số có phần nguyên lớn hơn thì số đó lớn hơn).
- Nhóm các số thập phân âm:
+ Số đối của các số −5,24; −4,125; −0,26 lần lượt là 5,24; 4,125; 0,26.
+ Chữ số hàng phần mười của các số 5,24; 4,125; 0,26 lần lượt là 5; 4; 0.
+ Ta so sánh phần nguyên của các số trên:
Vì 0 < 4 < 5 nên 0,26 < 4,125 < 5,24. Suy ra −0,26 > −4,125 > −5,24.
Do đó 5,4 > 1,41 > 0,6 > 0,22 > −0,26 > −4,125 > −5,24.
Vậy các số được sắp xếp thứ tự giảm dần là: 12,79; 5,17; 0,6; 0,22; −0,26; −4,125; −5,24.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:
* Phân loại:
- Nhóm các số thập phân dương: 0,124; 0,12.
- Nhóm các số thập phân âm: −4,23; −0,12; −0,02; −0,001; −1,28.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương:
+ Hai số 0,124; 0,12 có cùng phần nguyên nên ta so sánh phần thập phân.
+ Hàng phần mười và hàng phần trăm của hai số này đều bằng nhau.
+ Ta so sánh hàng phần nghìn của hai số, hàng phần nghìn của 0,124 và 0,12 lần lượt là 4 và 0. Vì 4 > 0 nên 0,124 > 0,12.
- Nhóm các số thập phân âm:
+ Số đối của các số −4,23; −0,12; −0,02; −0,001; −1,28 lần lượt là 4,23; 0,12; 0,02; 0,001; 1,28.
+ Số 4,23 có phần nguyên là 4;
+ Số 1,28 có phần nguyên là 1;
+ Các số 0,12; 0,02; 0,001 đều có phần nguyên là 0 nên ta so sánh phần thập phân của các số
+) Số 0,12 có hàng phần mười là 1.
+) Các số 0,02; 0,001 đều có hàng phần mười là 0, ta tiếp tục so sánh hàng phần trăm của hai số, hàng phần trăm của 0,02; 0,001 lần lượt là 2 và 0. Vì 2 > 0 nên 0,02 > 0,001.
Do đó 4,23 > 1,28 > 0,02 > 0,001 hay −4,23 < −1,28 < −0,02 < −0,001.
Từ đó ta suy ra −4,23 < −1,28 < −0,02 < −0,001 < 0,12 < 0,124 .
Vậy các số được sắp xếp thứ tự tăng dần là: −4,23; −1,28; −0,02; −0,001; 0,12; 0,124.

Tính phần trăm lương tối thiểu vùng I năm 2018 tăng so với năm 2017.
Lời giải:
Mức lương tối thiểu vùng I năm 2018 tăng so với năm 2017 là:
3 980 000 − 3 750 000 = 230 000 (đồng)
Phần trăm lương tối thiểu vùng I năm 2018 tăng so với năm 2017 là:
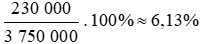
Vậy phần trăm lương tối thiểu vùng I năm 2018 tăng so với năm 2017 là khoảng 6,13%.
Lời giải:
Lượng điện năng tiêu thụ của tháng 3/2019 tăng so với tháng 2/2019 là:
2,38 − 1,65 = 0,73 (tỉ kWh)
Phần trăm lượng điện năng tiêu thụ tháng 3/2019 tăng so với tháng 2/2019 là:
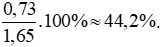
Vậy phần trăm lượng điện năng tiêu thụ tháng 3/2019 tăng so với tháng 2/2019 là 44,2%.
Lời giải:
Nếu không tính tiền phục vụ thì phần trăm số tiền người đó trả cho bữa ăn so với số tiền đã trả là:
100% − 10% = 90%.
Nếu không tính tiền phục vụ thì số tiền thực mà khách cần trả là:
2 750 000 . 90% = 2 475 000 (đồng).
Vậy nếu không tính tiền phục vụ thì số tiền thực mà khách cần trả cho bữa ăn là 2 475 000 đồng.
Lời giải:
Số tiền được giảm khi mua món hàng đó là:
8% . 250 000 = 20 000 (đồng)
Số tiền mà khách hàng phải trả cho cửa hàng khi mua món hàng đó sau khi đã được giảm giá là:
250 000 − 20 000 = 230 000 (đồng)
Vậy số tiền mà khách hàng phải trả cho cửa hàng khi mua món hàng đó sau khi đã được giảm giá là 230 000 đồng.
Lời giải:
Tổng số học sinh cả lớp là:
20 + 24 = 44 (học sinh).
Tỉ số phầm trăm số học sinh nữ và số học sinh cả lớp là:
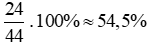
Vậy tỉ số phầm trăm số học sinh nữ và số học sinh cả lớp là 54,5%.
Lời giải:
Tổng số quần áo cửa hàng đã bán được trong một tháng là:
25 + 40 = 65 (chiếc).
Tỉ số phần trăm giữa số lượng áo so với tổng số hàng đã bán là:
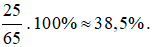
Vậy tỉ số phần trăm giữa số lượng áo so với tổng số hàng đã bán là 38,5%.
Bài 9 trang 62 sách bài tập Toán lớp 6 Tập 2: Làm tròn các số sau: −1254,5678; 542,1235
a) đến hàng phần mười;
b) đến hàng phần trăm;
c) đến hàng phần nghìn;
d) đến hàng đơn vị;
e) đến hàng chục.
Lời giải:
* Làm tròn số: −1254,5678
a) đến hàng phần mười
- Chữ số hàng phần mười của số −1254,5678 là 5.
- Chữ số bên phải liền nó là 6 > 5 nên chữ số hàng phần mười tăng lên một đơn vị là 6 và bỏ các chữ số từ hàng phần trăm trở đi.
Do đó, số −1254,5678 làm tròn đến hàng phần mười là: −1254,6.
b) đến hàng phần trăm:
- Chữ số hàng phần trăm của số −1254,5678 là 6.
- Chữ số bên phải liền nó là 7 > 5 nên chữ số hàng phần trăm tăng lên một đơn vị là 7 và bỏ các chữ số từ hàng phần nghìn trở đi.
Do đó, số −1254,5678 làm tròn đến hàng phần trăm là: −1254,57.
c) đến hàng phần nghìn
- Chữ số hàng phần nghìn của số −1254,5678 là 7.
- Chữ số bên phải liền nó là 8 >5 nên chữ số hàng phần nghìn tăng lên một đơn vị là 8 và bỏ đi chữ số hàng phần chục nghìn.
Do đó, số −1254,5678 làm tròn đến hàng phần nghìn là: −1254,568.
d) đến hàng đơn vị
- Chữ số hàng đơn vị của số −1254,5678 là 4.
- Chữ số bên phải liền nó là 5 nên chữ số hàng đơn vị tăng lên một đơn vị là 5 đồng thời bỏ các chữ số ở phần thập phân.
Do đó, số −1254,5678 làm tròn đến hàng đơn vị là: −1255.
e) đến hàng chục:
- Chữ số hàng chục của số −1254,5678 là 5.
- Chữ số bên phải liền nó là 4 < 5 nên chữ số hàng chục giữ nguyên là 5 đồng thời thay chữ số hàng đơn vị bằng số 0 và bỏ tất cả các chữ số ở phần thập phân.
Do đó, số −1254,5678 làm tròn đến hàng chục là: −1250.
Vậy số −1254,5678 làm tròn đến hàng phần mười, phần trăm, phần nghìn, hàng đơn vị và hàng chục lần lượt là −1254,6; −1254,57; −1254,568; −1255; −1250.
* Làm tròn số: 542,1235
a) đến hàng phần mười
- Chữ số hàng phần mười của số 542,1235 là 1.
- Chữ số bên phải liền nó là 2 < 5 nên chữ số hàng phần mười giữ nguyên là 1 và bỏ các chữ số từ hàng phần trăm trở đi.
Do đó, số 542,1235 làm tròn đến hàng phần mười là: 542,1.
b) đến hàng phần trăm:
- Chữ số hàng phần trăm của số 542,1235 là 2.
- Chữ số bên phải liền nó là 3 < 5 nên chữ số hàng phần trăm giữ nguyên là 2 và bỏ các chữ số từ hàng phần nghìn trở đi.
Do đó, số 542,1235 làm tròn đến hàng phần trăm là: 542,12.
c) đến hàng phần nghìn
- Chữ số hàng phần nghìn của số 542,1235 là 3.
- Chữ số bên phải liền nó là 5 5 nên chữ số hàng phần nghìn tăng lên một đơn vị là 4 và bỏ đi chữ số hàng phần chục nghìn.
Do đó, số 542,1235 làm tròn đến hàng phần nghìn là: 542,124.
d) đến hàng đơn vị
- Chữ số hàng đơn vị của số 542,1235 là 2.
- Chữ số bên phải liền nó là 1 < 5 nên chữ số hàng đơn vị giữ nguyên là 2 đồng thời bỏ các chữ số ở phần thập phân.
Do đó, số 542,1235 làm tròn đến hàng đơn vị là: 542.
e) đến hàng chục
- Chữ số hàng chục của số 542,1235 là 4.
- Chữ số bên phải liền nó là 2 < 5 nên chữ số hàng chục giữ nguyên là 4 đồng thời thay chữ số hàng đơn vị bằng số 0 và bỏ tất cả các chữ số ở phần thập phân.
Do đó, số 542,1235 làm tròn đến hàng chục là: 540.
Vậy số 542,1235 làm tròn đến hàng phần mười, phần trăm, phần nghìn, hàng đơn vị và hàng chục lần lượt là 542,1; 542,12; 542,124; 542; 540.
π = 3,1415926535897932384626433...
Hãy làm tròn số π:
a) đến hàng phần mười;
b) đến hàng phần trăm;
c) đến hàng phần nghìn;
d) đến hàng đơn vị.
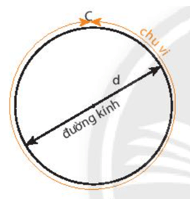
Chu vi của một đường tròn lớn hơn khoảng 3 lần so với đường kính.
Giá trị chính xác gọi là số π.
Lời giải:
Làm tròn số: π = 3,1415926535897932384626433...
a) đến hàng phần mười
- Chữ số hàng phần mười của số π là 1.
- Chữ số bên phải liền nó là 4 < 5 nên chữ số hàng phần mười giữ nguyên là 1 và bỏ các chữ số từ hàng phần trăm trở đi.
Do đó, số π làm tròn đến hàng phần mười là: 3,1.
b) đến hàng phần trăm:
- Chữ số hàng phần trăm của số π là 4.
- Chữ số bên phải liền nó là 1 < 5 nên chữ số hàng phần trăm giữ nguyên là 4 và bỏ các chữ số từ hàng phần nghìn trở đi.
Do đó, số π làm tròn đến hàng phần trăm là: 3,14.
c) đến hàng phần nghìn
- Chữ số hàng phần nghìn của số π là 1.
- Chữ số bên phải liền nó là 5 nên chữ số hàng phần nghìn tăng lên một đơn vị là 2 và bỏ đi chữ số hàng phần chục nghìn.
Do đó, số π làm tròn đến hàng phần nghìn là: 3,142.
d) đến hàng đơn vị
- Chữ số hàng đơn vị của số π là 3.
- Chữ số bên phải liền nó là 1 < 5 nên chữ số hàng đơn vị giữ nguyên là 3 đồng thời bỏ các chữ số ở phần thập phân.
Do đó, số π làm tròn đến hàng đơn vị là: 3.
Vậy số π làm tròn đến hàng phần mười, phần trăm, phần nghìn, hàng đơn vị lần lượt là 3,1; 3,14; 3,142; 3
Bài 11 trang 62 sách bài tập Toán lớp 6 Tập 2: Hãy ước lượng kết quả các phép tính sau:
a) (39,24 + 16,08) . 2;
b) (5,86 : 1,78) + (14,98 : 1,88).
Lời giải:
a) Ta có: 39,24 ≈ 39; 16,08 ≈ 16.
Do đó (39,24 + 16,08) . 2 ≈ (39 + 16) . 2 = 55 . 2 = 110.
b) Ta có: 5,86 ≈ 6; 1,78 ≈ 2; 14,98 ≈ 15; 1,88 ≈ 2.
Do đó (5,86 : 1,78) + (14,98 : 1,88) ≈ (6 : 2) + (15 : 2 ) = 3 + 7,5 = 10,5.
a) 0,246 . (−5,128) = −3,261 488;
b) −7,105 + 4,23 = −5,682.
Lời giải:
a) Ta có: 0,246 ≈ 0,25; −5,128 ≈ −5.
Do đó 0,246 . (−5,128) ≈ 0,25 . (−5) = −1,25, kết quả khoảng −1.
Vậy phép tính 0,246 . (−5,128) = −3,261 488 sai.
b) Ta có: −7,105 ≈ −7; 4,23 ≈ 4.
Do đó −7,105 + 4,23 ≈ (−7) + 4 = −3, kết quả khoảng −3.
Vậy phép tính −7,105 + 4,23 = −5,682 sai.
Lời giải:
Tỉ lệ của bản đồ là tỉ lệ giữa kích thước trên bản đồ so với kích thước thật (cùng một đơn vị đo).
Đổi: 61,9 km = 6 190 000 cm.
Tỉ lệ giữa kích thước trên bản đồ so với kích thước thật là:
3,1 : 6 190 000 ≈ 3 : 6 000 000 = 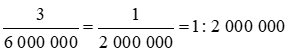
Vậy tỉ lệ bản đồ là 1 : 2 000 000.
Lời giải:
Tỉ lệ 1 : 5 000 000 nghĩa là 1 cm trên bản đồ tương ứng với 5 000 000 cm trên thực tế.
Chiều dài thực tế của cao tốc là:
1,02 . 5 000 000 = 5100 000 (cm) = 51 (km).
Vậy chiều dài thực tế của cao tốc là 51 km.
Lời giải:
Tỉ lệ phần trăm của đường trong dung dịch nước đường là tỉ lệ phần trăm giữa khối lượng đường và khối lượng dung dịch.
Khối lượng dung dịch đường là:
40 + 160 = 200 (g)
Tỉ lệ phần trăm của đường trong dung dịch nước đường là:
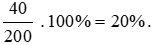
Vậy tỉ lệ phần trăm đường trong dung dịch nước đường là 20%.
Lời giải:
Bài toán đưa về tìm a, biết a bằng 40% của 200.
Khối lượng cà phê tinh chất trong một hộp có chứa 200 g cà phê hòa tan đó là:
200 . 40% = 80 (g)
Vậy khối lượng cà phê tinh chất trong một hộp có chứa 200 g cà phê hòa tan đó là 80 g.
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Tỉ số và tỉ số phần trăm

