Sách bài tập Toán 6 Bài ôn tập cuối chương 3
Lời giải:
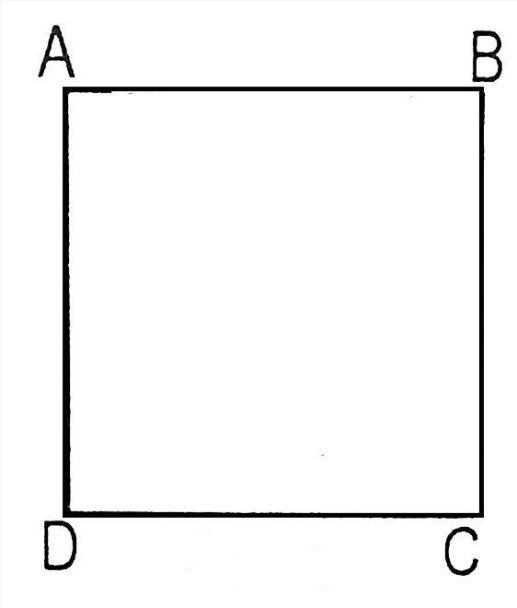
Vì ABCD là hình vuông nên AB = CD = AD = BC = 9 cm.
Vậy AD = CD = 9cm.
Lời giải:
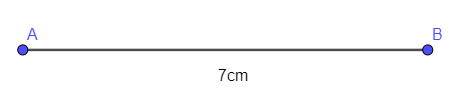
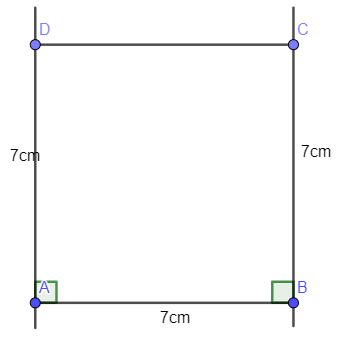
- Dùng thước vẽ đoạn thẳng AB = 7 cm:
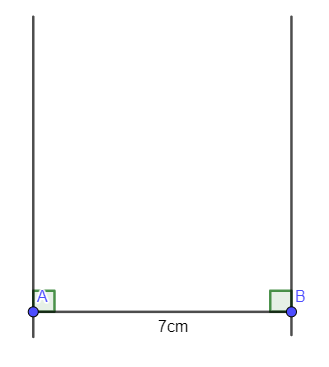
- Dùng eke và thước vẽ các đường thẳng vuông góc với AB tại A và B:
- Trên đường vuông góc tại A lấy điểm D với AD = 7 cm. Trên đường vuông góc tại B lấy điểm C với BC = 7 cm:
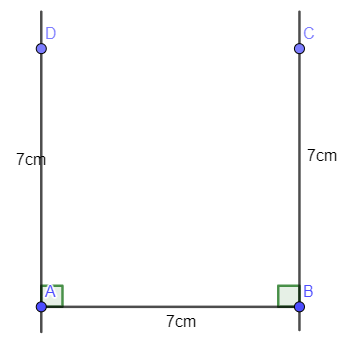
- Kẻ đoạn thẳng nối C và D ta được tứ giác ABCD là hình vuông có độ dài cạnh 7 cm:
- Sử dụng compa để so sánh hai đường chéo:
Mở compa tâm A bán kính AC vẫn giữ nguyên compa ta đặt một đầu compa vào điểm B và đầu còn lại ta thấy trùng khít với điểm D. Như vậy hai đường chéo của hình vuông bằng nhau.
Lời giải:
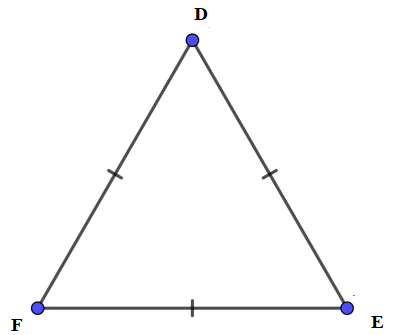
Vì tam giác DEF đều nên DE = EF = DF = 5 cm.
Vậy EF = DF = 5cm.
Lời giải:
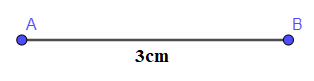
- Dùng thước vẽ đoạn thẳng AB = 3 cm:
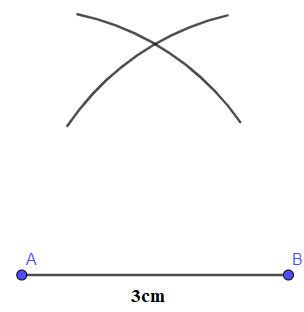
- Dùng compa vẽ các phần đường tròn cùng bán kính 3 cm và có tâm lần lượt là A, B:
- Hai phần đường tròn nói trên cắt nhau tại điểm C:
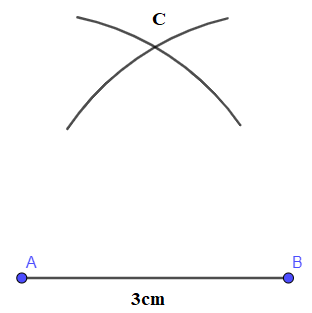
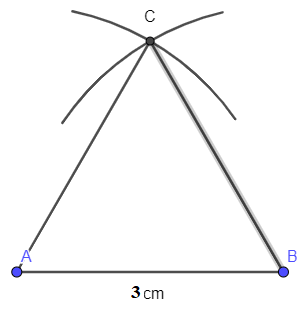
- Kẻ đoạn thẳng nối C và A, C và B ta có tam giác đều ABC với cạnh 3 cm
Lời giải:
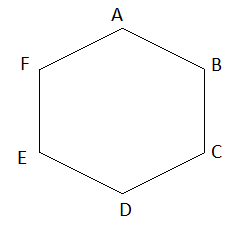
Vì ABCDEF là lục giác đều nên CD = AB = 8 cm; CF = AD = 16 cm.
Vậy CD = 8cm, CF = 16 cm.
Lời giải:

ABCD là hình chữ nhật nên:
AD = BC = 9 cm
CD = AB = 12 cm
AC = BD = 15 cm
Vậy AD = 9cm, CD = 12 cm, AC = 15cm.
Lời giải:
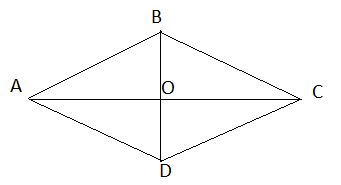
Ta có: ABCD là hình thoi nên:
AD = BC = CD = AB = 20 cm
OA = OC = 16 cm
Suy ra AC = OA + OC = 16 + 16 = 32 cm
OB = OD = 12 cm
Suy ra BD = OB + OD = 12 + 12 = 24 cm
Vậy độ dài cạnh của hình thoi là 20cm và độ dài hai đường chéo lần lượt là 32cm và 24cm.
Lời giải:
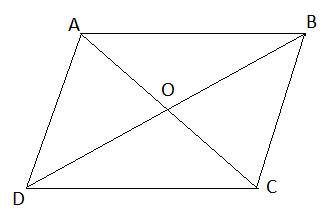
ABCD là hình bình hành nên:
BC = AD = 10 cm
CD = AB = 16 cm
AC = 2.OC = 2.6 = 12 cm
Vậy BC = 10 cm, CD = 16 cm, AC = 12cm.
Lời giải:
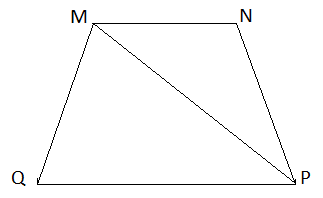
MNPQ là hình thang cân nên:
MQ = NP = 6 cm
NQ = MP = 10 cm
Vậy MQ = 6cm, NQ = 10 cm.
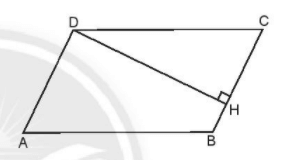
Lời giải:
Vì ABCD là hình bình hành nên AD = BC = 6cm, AB = CD = 10 cm.
Chu vi hình bình hành là: AB + BC + CD + AD = 6 + 6 + 10 + 10 = 32 (cm)
Diện tích hình bình hành là: BC.DH = 6.9 = 54 (cm2)
Vậy chu vi hình bình hành ABCD là 32cm, diện tích hình bình hành ABCD là 54 cm2.
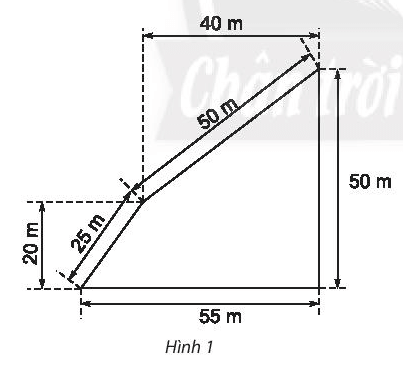
Lời giải:
Hình 1:
Chu vi hình 1 là: P = 25 + 50 + 50 + 55 = 180 (m)
Để tính diện tích của hình này, ta chia hình này thành các hình như sau:
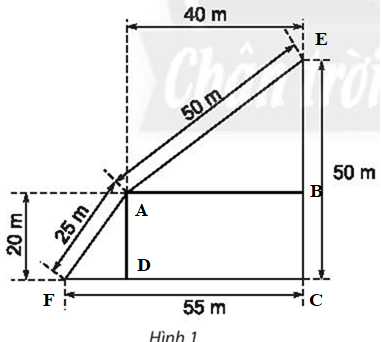
Theo hình vẽ, ta có: AD = BC = 20 m, AB = DC = 40 m, DF = CF – DC = 55 – 40 = 15 m, BE = CE – BC = 50 – 20 = 30 m.
Diện tích hình chữ nhật ABCD là: AB.AD = 40.20 = 800 (m2).
Diện tích tam giác ADF là: AD.DF : 2 = 20.15:2 = 150 (m2).
Diện tích tam giác ABE là: AB.BE : 2 = 40.30: 2 = 600 (m2).
Diện tích của hình đã cho là: 800 + 150 + 600 = 1 550 (m2).
Vậy diện tích của hình đã cho là 1 550 m2.
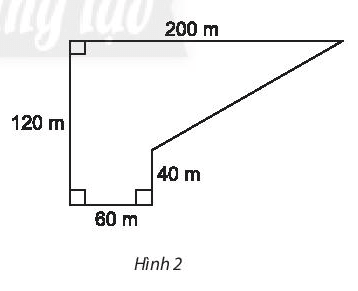
Hình 2:
Cách 1: Có thể chia hình đã cho thành hình chữ nhật ABCD và hình thang CDEF như sau:
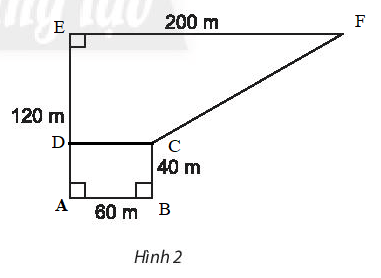
Ta có: AD = BC = 40 m, AB = CD = 60m, DE = AE – AD = 120 – 40 = 80m.
Diện tích hình chữ nhật ABCD là: AB.BC = 60.40 = 2 400 (m2).
Diện tích hình thang CDEF là: (CD + EF).DE:2 = (60 + 200).80:2 = 10 400 (m2).
Diện tích của hình đã cho là: 2 400 + 10 400 = 12 800 (m2).
Vậy chu vi, diện tích của hình đã cho lần lượt là 180 m, 12 800 m2.
Cách 2: Có thể chia hình thành hình chữ nhật MNPQ và hình tam giác PHK như sau:
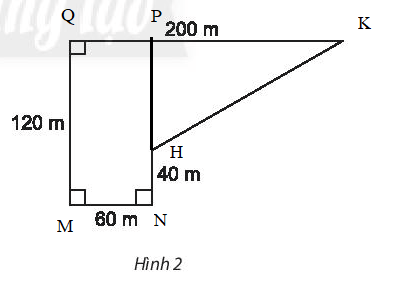
Ta có: PQ = MN = 60 m, PH = PN – NH = 120 – 40 = 80 m, PK = QK – PQ = 200 – 60 = 140 m.
Diện tích hình chữ nhật MNPQ là: MN.MQ = 60. 120 = 7 200 (2).
Diện tích hình tam giác PHK là: PH.PK = 80.140:2 = 5 600 (2).
Diện tích hình đã cho là: 7 200 + 5 600 = 12 800 (2).
Vậy chu vi, diện tích của hình đã cho lần lượt là 180 m và 12 800 2.
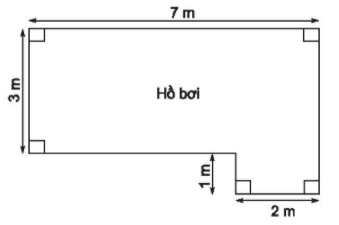
Lời giải:
Chu vi của hồ bơi là:
P = 3 + 7 + 4 + 2 + 1 + 5 = 22 (m)
Ta sẽ chia hình thành các hình nhỏ để dễ dàng tính diện tích:
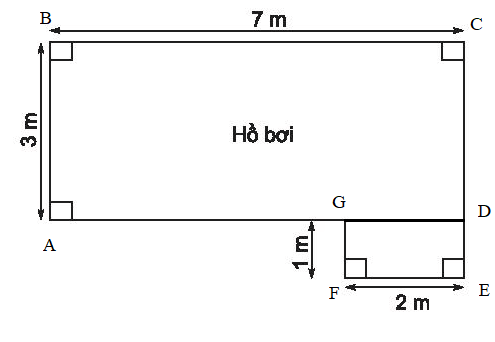
Diện tích của hình chữ nhật ABCD là: AB.BC = 3.7 = 21 (m2).
Diện tích của hình chữ nhật DEFG là: EF.GF = 2.1 = 2 (2).
Diện tích của hình đã cho là: 21 + 2 = 23 (2).
Vậy chu vi của hình đã cho là 22 m và diện tích của hình đã cho là 23 2.
(Có thể chia hình đã cho theo nhiều cách khác nhau để tính toán).
Bài 13 trang 78 sách bài tập Toán lớp 6 Tập 1: Tính diện tích của hình sau:
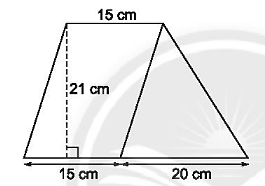
Lời giải:
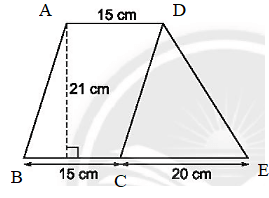
Diện tích hình bình hành ABCD là: 15.21 = 315 (cm2).
Diện tích của tam giác CDE là: 20.21:2 = 210 (cm2).
Diện tích của hình đã cho là: 315 + 210 = 525 (cm2).
Vậy diệc tích của hình đã cho là 525 cm2.
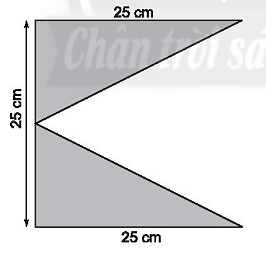
Bài 14 trang 78 sách bài tập Toán lớp 6 Tập 1: Tính diện tích của hình sau:
Lời giải:
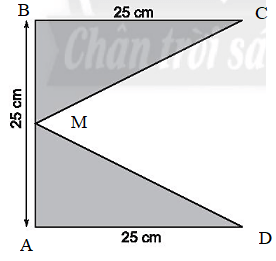
Ta có: AM = BM = 25:2 = 12,5 cm.
Ta nhận thấy diện tích hai tam giác ADM và BCM bằng nhau vì AM = MB, AD = BC nên diện tích của hình đã cho bằng hai lần diện tích tam giác ADM và bằng: 2.(AD.AM:2) = 2.(25.12,5:2) = 25.12,5 = 312,5 (cm2).
Vậy diện tích hình đã cho là 312,5 cm2.
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 2. Hình thoi - Hình chữ nhật - Hình bình hành - Hình thang cân
Bài 3. Chu vi và diện tích một số hình trong thực tiễn
Bài 1. Thu thập và phân loại dữ liệu

