Sách bài tập Toán 6 Bài 2: Hình thoi - Hình chữ nhật - Hình bình hành - Hình thang cân
Lời giải:
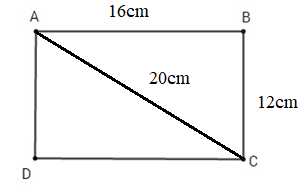
ABCD là hình chữ nhật nên AD = BC = 12 cm; DC = AB = 16 cm; AC = BD = 20 cm.
Vậy AD = 12cm, DC = 16cm, AC = 20cm.
Lời giải:
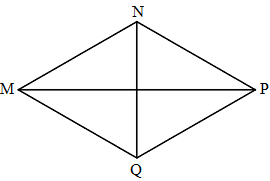
MNPQ là hình thoi nên PQ = MN = NP = MQ = 10 cm.
Vậy MN = NP = MQ = 10 cm.
Lời giải:
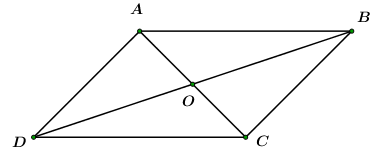
ABCD là hình bình hành nên:
CD = AB = 8 cm; BC = AD = 5cm; OA = OC = 3 cm nên AC = 6 cm.
Vậy CD = 8cm, BC = 5cm, AC = 6cm.
Lời giải:
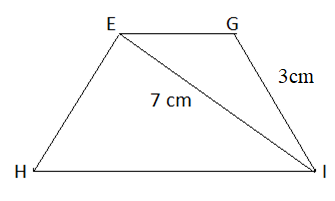
Vì EGIH là hình thang cân nên:
Hai cạnh bên bằng nhau: EH = GI = 3 cm;
Hai đường chéo bằng nhau: GH = EI = 7 cm
Vậy EH = 3cm, GH = 7cm.
Lời giải:
Hướng dẫn cách ghép:
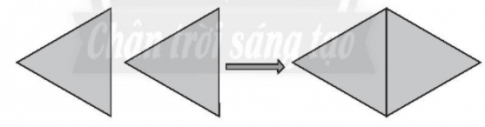
Lời giải:
Làm theo hướng dẫn sau:
Sẽ ghép chiều rộng 3cm của hình chữ nhật với cạnh góc vuông có độ dài 3cm của tam giác vuông, ta sẽ được hình thang cân cần tìm.
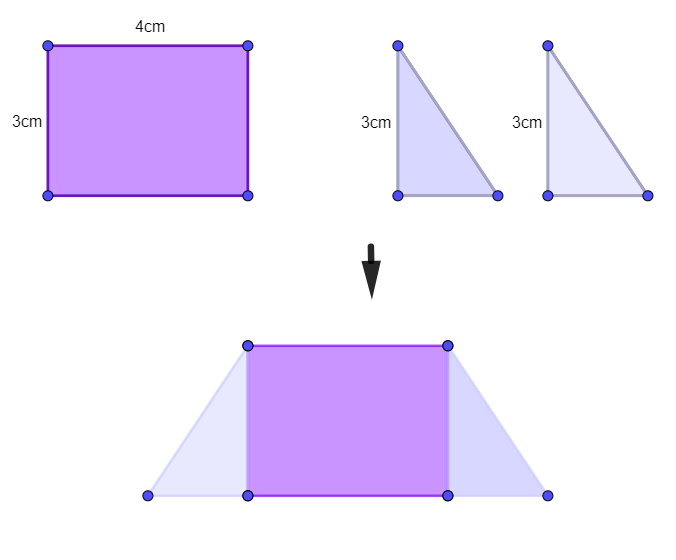
Lời giải:
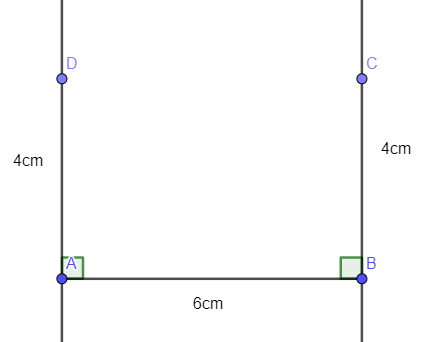
- Dùng thước thẳng vẽ đoạn AB = 6 cm:
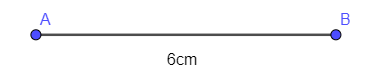
- Dùng eke và thước thẳng kẻ đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AB tại A
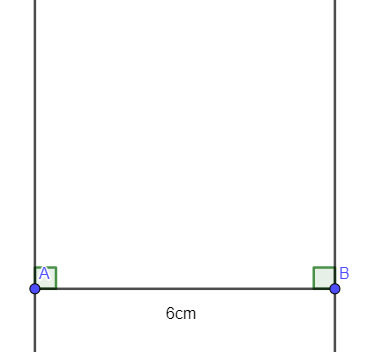
- Trên đường thẳng vuông góc với AB tại A, ta lấy điểm D sao cho AD = 4cm, trên đường thẳng vuông góc với AB tại B, ta lấy điểm C sao cho BC = 4cm.
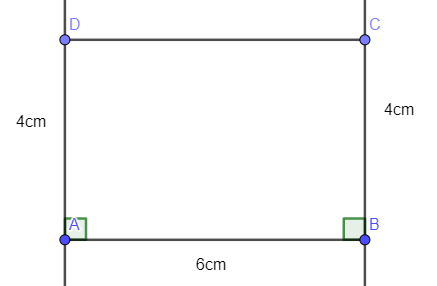
- Nối D với C ta được tứ giác ABCD là hình chữ nhật cần vẽ:
Lời giải:
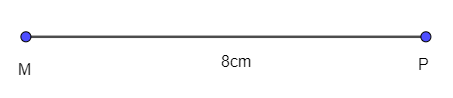
- Dùng thước thẳng vẽ đoạn thẳng MP = 8 cm:
- Dùng compa vẽ đường tròn tâm M bán kính 5 cm rồi vẽ đường tròn tâm P bán kính 3 cm. Hai đường tròn nên cắt nhau tại hai điểm N và Q:
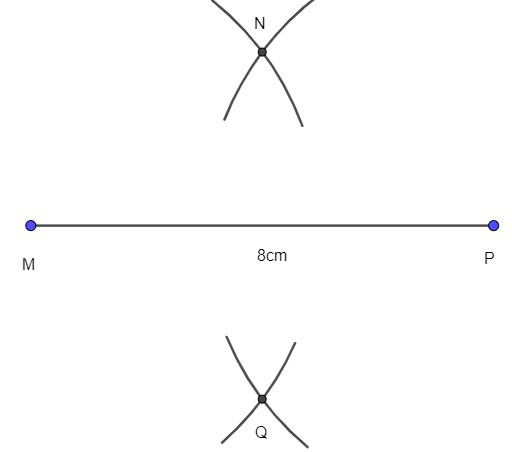
- Nối N với M, N với P, Q với P ta được tứ giác MNPQ là hình thoi cần vẽ.
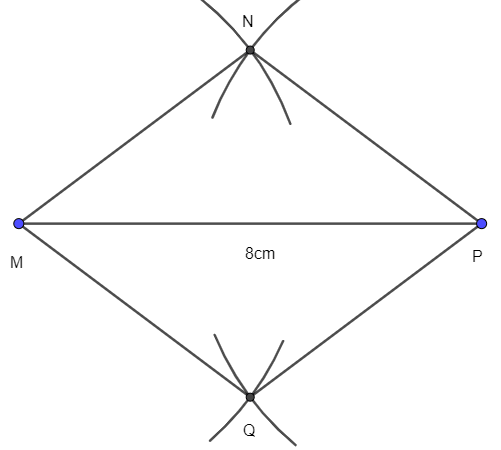
Lời giải:
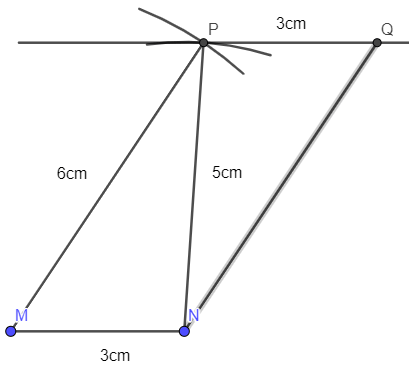
- Dùng thước thẳng vẽ đoạn MN = 3 cm:
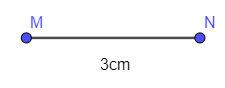
- Dùng compa vẽ một phần đường tròn tâm M bán kính 6 cm. Vẽ một phần đường tròn tâm N bán kính 5 cm. Hai phần đường tròn trên cắt nhau tại điểm P:
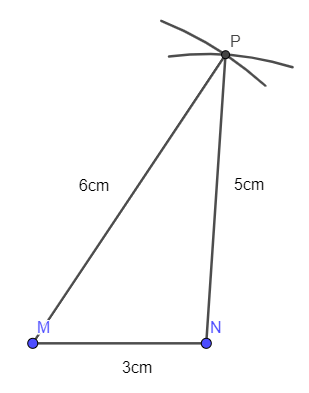
- Nối N với P. Từ M kẻ đường thẳng MQ song song với NP và MQ = 5 cm:
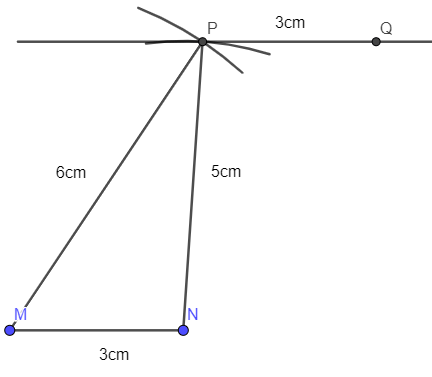
- Nối P với Q ta được tứ giác MNPQ là hình bình hành cần vẽ.
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 1. Hình vuông - Tam giác đều - Lục giác đều
Bài 3. Chu vi và diện tích một số hình trong thực tiễn
Bài 1. Thu thập và phân loại dữ liệu

