Khám phá 3 trang 74 Chuyên đề Toán 11:
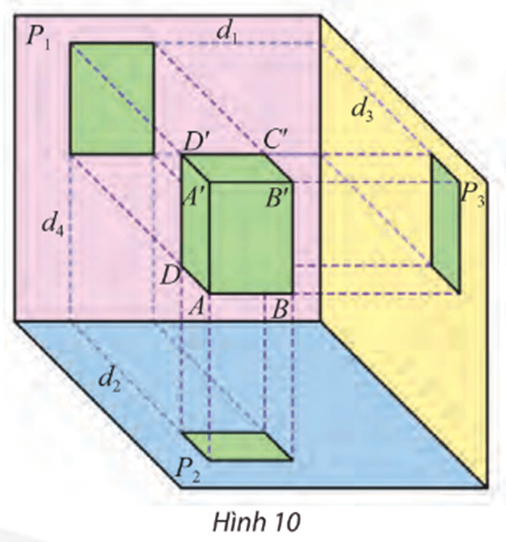
Quan sát Hình 10 và cho biết:
– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật, cạnh nào song song
với một trong ba mặt phẳng chiếu (P1), (P2), (P3)?
– Tìm hai giao tuyến của (P1) và (P2) với mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2).
– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật ABCD.A’B’C’D’, ta có:
⦁ Cạnh AB song song với các mặt phẳng chiếu (P1) và (P2);
⦁ Cạnh AA’ song song với các mặt phẳng chiếu (P1) và (P3);
⦁ Cạnh AD song song với các mặt phẳng chiếu (P2) và (P3).
Vậy cả ba cạnh AB, AA’ và AD của hình hộp chữ nhật đều song song với một trong ba mặt phẳng chiếu (P1), (P2) và (P3).
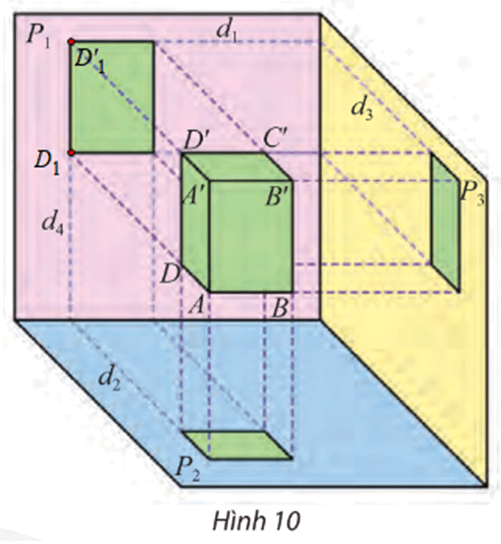
– Xác định hai giao tuyến của (P1) và (P2) với mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2):
Ta có AD ⊥ AA’ (do ABCD.A’B’C’D’ là hình hộp chữ nhật).
Mà AA’ // (P1).
Suy ra AD ⊥ (P1).
Do đó (AA’D’D) ⊥ (P1).
Chứng minh tương tự, ta được (AA’D’D) ⊥ (P2).
Vì vậy mặt phẳng đi qua điểm D và vuông góc với cả (P1) và (P2) là (AA’D’D).
Gọi D1, D1’ lần lượt là hình chiếu vuông góc của các điểm D, D’ lên mặt phẳng (P1).
Suy ra D1, D1’∈ (AA’D’D) và D1, D1’∈ (P1).
Do đó hay d4 = (AA’D’D) ∩ (P1).
Chứng minh tương tự, ta được d2 = (AA’D’D) ∩ (P2).
Vậy d4, d2 lần lượt là hai giao tuyến cần tìm.
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Đường đi Euler và đường đi Hamilton
Bài 3: Bài toán tìm đường đi ngắn nhất