Giải Chuyên đề Tin học 11 Bài 3: Thực hành giải toán theo kĩ thuật đệ quy
Lời giải:
Khi áp dụng kĩ thuật giải đệ quy để giải các bài toán, cần lưu ý đến điều kiện kết thúc đệ quy: Cần xác định điều kiện để thoát khỏi vòng lặp đệ quy, nếu không sẽ gây ra lỗi vô hạn lặp lại.
Luyện tập
Luyện tập 1 trang 18 Chuyên đề Tin học 11: Mô tả các bước tính gcd (93,60)
Lời giải:
|
STT |
a |
b |
a%b |
Ghi chú |
|
1 |
93 |
60 |
33 |
|
|
2 |
60 |
33 |
27 |
|
|
3 |
33 |
27 |
6 |
|
|
4 |
27 |
6 |
3 |
|
|
5 |
6 |
3 |
0 |
|
|
6 |
3 |
0 |
|
Nếu b = 0 thì dừng lại, thông báo ƯCLN = a |
Lời giải:
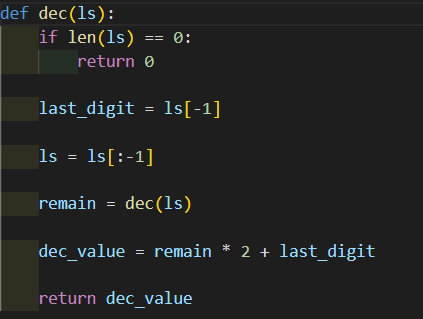
Để chuyển đổi số nhị phân sang hệ thập phân, ta có thể sử dụng kĩ thuật đệ quy như sau:
Vận dụng
Hãy viết lại chương trình trên theo kĩ thuật đệ quy.
Lời giải:
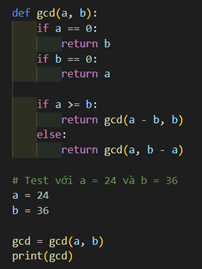
Lời giải:
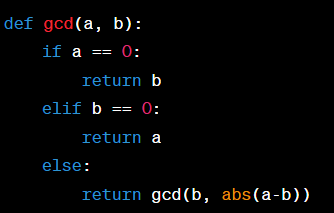
Bước cơ sở của đệ quy sẽ là trường hợp a hoặc b bằng 0, trong trường hợp này kết quả sẽ là giá trị khác 0 của a hoặc b.
Lời giải:
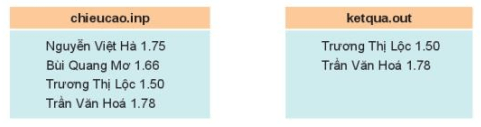
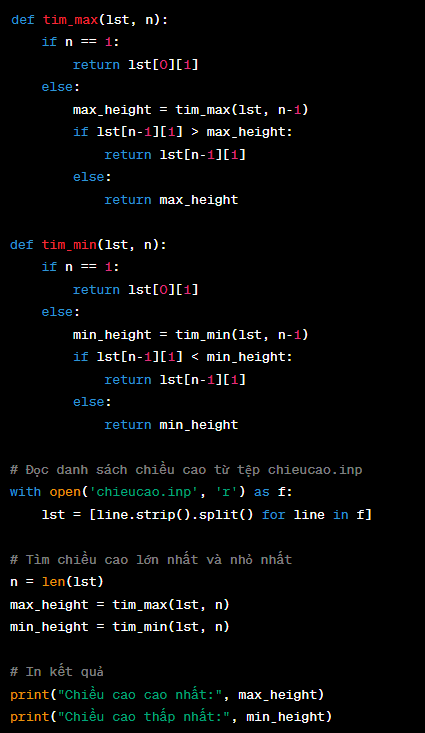
Để giải quyết yêu cầu này, ta có thể sử dụng kĩ thuật đệ quy để tìm chiều cao lớn nhất và nhỏ nhất trong danh sách.
Đầu tiên, ta đọc danh sách chiều cao từ tệp chieucao.inp. Tiếp theo, ta sử dụng hàm đệ quy để tìm chiều cao lớn nhất và nhỏ nhất.
Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 2: Thiết kế thuật toán đệ quy