Giải Chuyên đề Tin học 11 Bài 13: Kĩ thuật duyệt quay lui
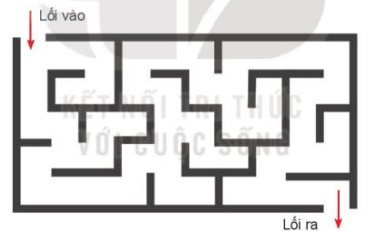
Hình 13.1. Mê cung
Trong trò chơi mê cung (xem hình) em cần tìm một đường đi xuất phát từ lối vào và ra khỏi mê cung tại lối ra. Em có đề xuất gì để giải bài toán này.
Lời giải:
Đề xuất: Xuất phát từ vị trí gốc, thuật toán sẽ gọi hàm tìm bước đi tiếp theo. Nếu thực hiện được một bước đi thì gọi lại hàm để tìm bước đi tiếp theo. Nếu không tìm thấy đường đi thì cần "quay lui" về vị trí trước đó để tìm đường đi khác. Cứ như vậy cho đến khi ra được khỏi mê cung
1. Kĩ thuật duyệt quay lui
Lời giải:
Ý tưởng của thuật toán duyệt quay lui là luôn tìm cách đi tiếp theo. Xuất phát từ vị trí gốc, thuật toán sẽ gọi hàm tìm bước đi tiếp theo. Nếu thực hiện được một bước đi thì gọi lại hàm để tìm bước đi tiếp theo. Nếu không tìm thấy đường đi thì cần "quay lui" về vị trí trước đó để tìm đường đi khác. Thuật toán sẽ sử dụng kĩ thuật đệ quy khi gọi hàm cho bước đi tiếp theo.
Lời giải:
Khi đã thực hiện hết các bước lặp tại dòng 2 ở trên thì hàm không dừng. Nếu đã đến đích thì thông báo tìm thấy thấy nghiệm tại dòng thứ 7, nếu chưa tìm thấy thì gọi đệ quy lại hàm gốc để đi tiếp tại dòng 10. Nếu không thể đi tiếp thì quay lui tại dòng 11, xóa dấu vết và quay lại vòng lặp 2.
Câu hỏi 2 trang 57 Chuyên đề Tin học 11: Lệnh gọi hàm chính của chương trình trên là gì?
Lời giải:
Lệnh gọi hàm chính của chương trình trên là dòng số 2, lặp trên tập hợp các khả năng có thể đi tiếp
Lời giải:
Lệnh “Nếu thấy
2. Mô hình tổng quát của thuật toán duyệt quay lui
Lời giải:
Mô hình thuật toán quay lui tổng quát quy định việc tìm trên các dãy số nguyên x1, x2,...xk sử dụng lệnh gọi đệ quy để mô tả bước đi tiếp theo với k + 1, nếu không tìm được bước đi tiếp theo thì quay lui để tìm hướng đi khác.
Mô hình tổng quát duyệt quay lui sử dụng đệ quy như sau:
Câu hỏi 1 trang 59 Chuyên đề Tin học 11: Trạng thái "quay lui" của thuật toán trên nằm ở đâu?
Lời giải:
Trong quá trình thực hiện thuật toán, khi tìm được một giải pháp không hợp lệ hoặc không có giải pháp, chương trình sẽ quay lui ngược trở về trạng thái trước đó và tiếp tục thử các giá trị khác cho các biến trạng thái. Khi quay lui, chương trình sẽ trả lại các giá trị đã được duyệt trước đó và trở về trạng thái trước đó để thử các giá trị khác. Quá trình quay lui này sẽ tiếp tục cho đến khi tìm được giải pháp hoặc đã thử tất cả các giá trị khả dĩ cho các biến trạng thái.
Lời giải:
Có thể đếm tất cả các nghiệm từ thuật toán duyệt quay lui dùng đệ quy bằng cách sử dụng biến đếm và tăng giá trị của biến này mỗi khi tìm được một nghiệm hợp lệ. Khi kết thúc thuật toán, giá trị của biến đếm sẽ là số lượng nghiệm tìm được.
3. Bài toán sinh xâu nhị phân
Lời giải:
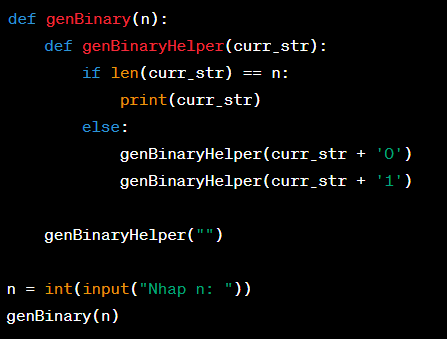
Để thiết kế chương trình sinh tất cả các dãy nhị phân độ dài n bằng kĩ thuật quay lui, ta có thể sử dụng đệ quy để thêm lần lượt các số 0 và 1 vào dãy nhị phân.
Bước 1: Viết hàm để sinh dãy nhị phân độ dài n:
Bước 2: Gọi hàm generate_binary_sequence với độ dài của dãy nhị phân cần sinh:
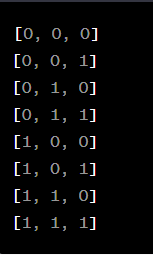
Thu được kết quả:
Câu hỏi 1 trang 60 Chuyên đề Tin học 11: Trong chương trình 1, động tác “quay lui” nằm ở đâu?
Lời giải:
Trong chương trình 1, động tác “quay lui” nằm ở dòng 7: genBinary (A, k+1)
Lời giải:
- Lệnh A.pop() tại dòng 8 của chương trình 2 nhằm xóa phần tử đã nhập từ bước trước khi quay lui
- Vì ở chương trình 1, dãy A được thiết lập từ trước có đủ n phần tử nên tại bước này chỉ là lệnh gán giá trị và không cần dùng lệnh pop()
- Ở Chương trình 2, dãy A ban đầu là dãy rộng, do đó A được bổ sung dần. Sau khi kết thúc lệnh gọi đệ quy ở dòng 7 cần gọi lệnh pop() ở dòng 8.
Luyện tập
Lời giải:
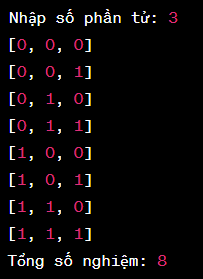
Biến count được sử dụng để đếm số lượng xâu nhị phân được sinh ra, và được khởi tạo là 0. Khi một xâu nhị phân được in ra, giá trị của count sẽ được tăng lên 1. Cuối cùng, in ra giá trị của biến count để hiển thị tổng số nghiệm.
Ví dụ n= 3:
Lời giải:
Có thể sử dụng thuật toán quay lui như sau:
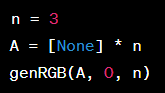
Ví dụ, nếu ta chạy đoạn code sau:
Kết quả sẽ là tất cả các xâu bao gồm 3 kí tự "R", "G" và "B":
Vận dụng
Lời giải:
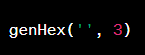
- Có thể sử dụng một hàm đệ quy, trong đó mỗi lần đệ quy, ta thêm một ký tự hex vào chuỗi kết quả và gọi đệ quy tiếp tục với số chỉ số còn lại.
Dưới đây là một ví dụ về cách thực hiện điều này bằng Python:
Ví dụ:
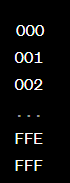
Kết quả:
Lời giải:
Sử dụng phép cộng chuỗi để có kết quả là chuỗi xâu nhị phân cần tìm
Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 11: Bài toán tìm kiếm theo kĩ thuật duyệt
Bài 12: Thực hành kĩ thuật duyệt cho bài toán tìm kiếm
Bài 14: Thực hành kĩ thuật duyệt quay lui
Bài 16: Thực hành thiết kế thuật toán theo kĩ thuật quay lui