Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho BD = DE = EC. Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC.

Chứng minh tứ giác DEFG là một hình vuông.

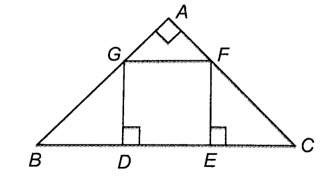
Do ∆ABC vuông cân tại A nên  $\widehat{B}=\widehat{C}=45°$.

Xét ∆GBD vuông tại D và ∆EFC vuông tại E có:

BD = EC;  $\widehat{B}=\widehat{C}$

Do đó ∆GBD = ∆FCE (cạnh góc vuông – góc nhọn kề)

Suy ra  $\widehat{DGB}=\widehat{EFC}$

Mà  $\widehat{B}+\widehat{DGB}=90°$ nên  $\widehat{DGB}=90°-\widehat{B}=90°-45°=45°$

Do đó  $\widehat{DGB}=\widehat{EFC}=45°$

Suy ra ∆GBD vuông cân tại D và ∆EFC vuông cân tại E.

Vì vậy GD = BD, EF = EC.

Mà  $BD=DE=EC=\frac{1}{3}BC$

Suy ra GD = DE = EF.

Do GD ⊥ BC, EF ⊥ BC nên GD // EF

Tứ giác GDEF có GD // EF, GD = EF nên GDEF là hình chữ nhật.

Lại có GD và DE là hai cạnh kề của hình chữ nhật GDEF bằng nhau nên GDEF là hình vuông.