Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM; nó cắt CD ở N. Đường thẳng qua N vuông góc với AM cắt BC ở P. Tính số đo của góc NAP.
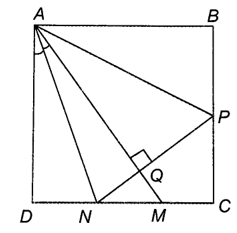
Đường thẳng NP ⊥ AM cắt AM ở Q.
Do ABCD là hình vuông nên ND ⊥ AD.
Xét DADN vuông tại D và DAQN vuông tại Q có:
AN là cạnh chung, ^NAD=^NAQ (do AN là tia phân giác của ^DAM)
Do đó ∆ADN = ∆AQN (cạnh huyền – góc nhọn)
Suy ra AD = AQ;
Mà AD = AB nên AQ = AB
Xét DAQP vuông tại Q và DABP vuông tại B có:
Cạnh AP chung; AQ = AB
Do đó ∆AQP = ∆ABP (cạnh huyền – cạnh góc vuông)
Suy ra ^QAP=^BAP.
Ta có: ^BAD=^DAN+^NAQ+^QAP+^BAP
Mà ^NAD=^NAQ; ^QAP=^BAP nên ta có:
^BAD=2(^NAQ+^PAQ)=2^NAPSuy ra ^NAP=12^DAB=12⋅90°