Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến, nghịch biến của chúng

Bài 6.6 trang 8 SBT Toán 10 Tập 2: Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến, nghịch biến của chúng.

a) $y=-\frac{1}{2}x+5$;

b) y = 3x²;

c) $y=\left\{\begin{array}{l}{x}^2(x\ge 0)\\ -x-1(x<0)\end{array}\right.$.

Trả lời

a)

Xét hàm số $y=-\frac{1}{2}x+5$

Ta có:

Khi x = 0 thì $y=-\frac{1}{2}.0+5=5$

Khi x = 10 thì $y=-\frac{1}{2}.10+5=5$

Do đó, đồ thị hàm số là đường thẳng đi qua hai điểm (0; 5) và (10; 0).

Ta có hình vẽ đồ thị hàm số:

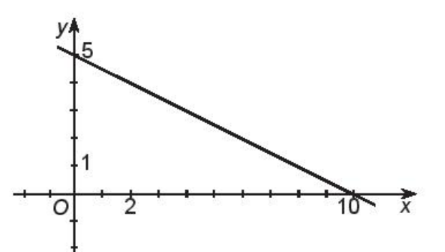
Tập giá trị của hàm số là: T = ℝ.

Đồ thị hàm số luôn đi xuống từ trái sang phải do đó hàm số nghịch biến trên ℝ.

b)

Xét hàm số y = 3x²

Ta có:

Trục đối xứng: x = 0

Đỉnh parabol là: (0; 0)

Khi x = 1 thì y = 3.1² = 3

Khi x = –1 thì y = 3.(–1)² = 3

Do đó, đồ thị hàm số là parabol có đỉnh (0; 0) đi qua hai điểm (1; 3) và (–1; 3)

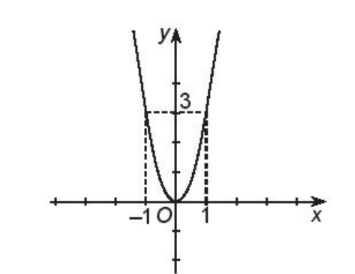
Tập xác định của hàm số là: T = [0; +∞).

Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; 0) nên hàm số nghịch biến trên khoảng (–∞; 0).

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (0; +∞) nên hàm số đồng biến trên khoảng (0; +∞).

c)

Xét hàm số $y=\left\{\begin{array}{l}{x}^2(x\ge 0)\\ -x-1(x<0)\end{array}\right.$

+) Khi x ≥ 0, ta có:

y = x²

Do đó, đồ thị hàm số là nửa parabol có trục đối xứng x = 0, đỉnh (0; 0), đi qua điểm (1; 1).

+) Khi x < 0, ta có:

y = –x – 1

Do đó, đồ thị hàm số là một phần đường thẳng đi qua điểm (0; –1) và (–1; 0).

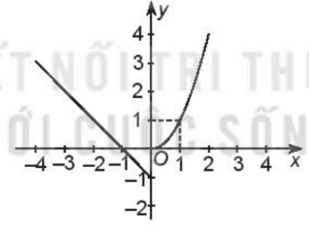
Tập giá trị của hàm số là: T = (–1; +∞)

Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; 0) nên hàm số nghịch biến trên khoảng (–∞; 0)

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (0; +∞) nên hàm số đồng biến trên khoảng (0; +∞).

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 14: Các số đặc trưng đo độ phân tán

Bài tập cuối chương 5

Bài 15: Hàm số

Bài 16: Hàm số bậc hai

Bài 17: Dấu của tam thức bậc hai

Bài 18: Phương trình quy về phương trình bậc hai