Tứ diện ABCD có AB ⊥ (BCD). Trong tam giác BCD vẽ đường cao BE và DF
Tứ diện ABCD có AB ⊥ (BCD). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng (ACD) vẽ DK vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng:
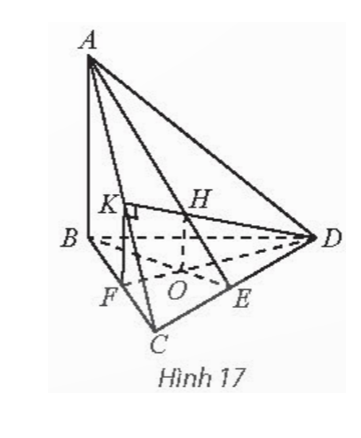
a) (ADC) ⊥ (ABE) và (ADC) ⊥ (DFK).

