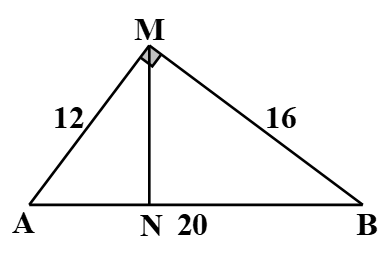
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn đặt tại \(A\) và \(B\) cách nhau \(20{\rm{\;cm}}\), dao động theo phương thẳng đứng và giống hệt nhau, tốc độ truyền sóng \({\rm{v}} = 25{\rm{\;cm}}/{\rm{s}}\). Trên mặt nước, \({\rm{M}}\) là điểm mà phần tử nước tại đó dao động với biên độ cực đại, \({\rm{MA}} = 12{\rm{\;cm}},{\rm{MB}} = 16{\rm{\;cm}}\). Điểm \({\rm{N}}\) thuộc đoạn \({\rm{AB}}\), đường thẳng \(\left( {\rm{\Delta }} \right)\) đi qua \({\rm{M}}\) và \({\rm{N}}\). Cho \({\rm{N}}\) di chuyển trên đoạn \({\rm{AB}}\) đến vị trí sao cho tổng khoảng cách từ hai nguồn đến đường thẳng \(\left( {\rm{\Delta }} \right)\) là lớn nhất, khi đó phần tử nước tại \({\rm{N}}\) dao động với biên độ cực đại và số điểm nằm yên trên đoạn \({\rm{AM}}\) nhiều hơn số điểm nằm yên trên đoạn \({\rm{AN}}\) là 4. Tần số dao động của hai nguồn sóng bằng

D. \(62,5{\rm{\;Hz}}\).

\[d\left( {A,\Delta } \right) + d\left( {B,\Delta } \right) \le NA + NB = AB\]

Dấu = xảy ra khi \(\left\{ \begin{array}{l}d\left( {A,\Delta } \right) = NA\\d\left( {B,\Delta } \right) = NB\end{array} \right. \Rightarrow MN \bot AB\) tại \(N\)

\(\Delta MAB\) vuông tại \(M \Rightarrow \)\(\left\{ \begin{array}{l}NA = \frac{{M{A^2}}}{{AB}} = \frac{{{{12}^2}}}{{20}}\\NB = \frac{{M{B^2}}}{{AB}} = \frac{{{{16}^2}}}{{20}}\end{array} \right.\)

\({k_N} - {k_M} = \frac{{NB - NA}}{\lambda } - \frac{{MB - MA}}{\lambda } = \frac{{\frac{{{{16}^2}}}{{20}} - \frac{{{{12}^2}}}{{20}}}}{\lambda } - \frac{{16 - 12}}{\lambda } = 4 \Rightarrow \lambda = 0,4cm\)

\(f = \frac{v}{\lambda } = \frac{{25}}{{0,4}} = 62,5Hz\). Chọn D