Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 2)^2 + y^2 = 1. a) Tìm tọa độ tâm đường tròn (C') là ảnh của đường tròn (C) qua Q( O, pi /2). b) Viết phương trình (C').
19
29/07/2024
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 2)2 + y2 = 1.
a) Tìm tọa độ tâm đường tròn (C') là ảnh của đường tròn (C) qua \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\).
b) Viết phương trình (C').
Trả lời
Lời giải:
Ta có (C): (x – 2)2 + y2 = 1. Suy ra đường tròn (C) có tâm I(2; 0) và bán kính R = 1.
Vì (C') là ảnh của đường tròn (C) qua phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) nên tâm I' của đường tròn (C') là ảnh của tâm I của đường tròn (C) qua phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\).
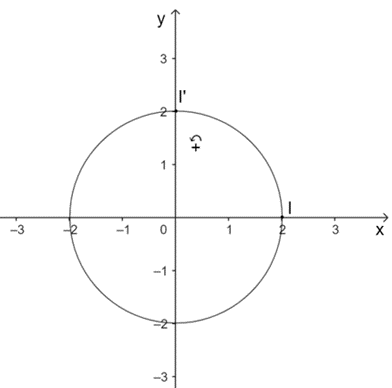
Vì I(2; 0) nên I'(0; 2).
b) Phép quay biến đường tròn thành đường tròn có cùng bán kính nên bán kính của đường tròn (C') là 1.
Vậy phương trình đường tròn (C') là x2 + (y – 2)2 = 1.
