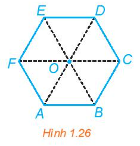
Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay Q_( O, pi /3), Q( O, - 2pi /3).

Trả lời

Lời giải:

Ta có: ABCDEF là lục giác đều nên $\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = 60^\circ = \frac{\pi }{3}$ và OA = OB = OC = OD = OE = OF.

Do đó, phép quay ${Q_{\left( {O,\frac{\pi }{3}} \right)}}$ biến các điểm A, C, E tương ứng thành các điểm B, D, F.

Vậy phép quay ${Q_{\left( {O,\frac{\pi }{3}} \right)}}$ biến tam giác ACE thành tam giác BDF.

Ta có: $\widehat {AOE} = \widehat {AOF} + \widehat {EOF} = \frac{{2\pi }}{3}$, tương tự $\widehat {COA} = \widehat {EOC} = \frac{{2\pi }}{3}$.

Vì OA = OE và góc quay $- \frac{{2\pi }}{3}$ nên phép quay ${Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}$ biến điểm A thành điểm E.

Vì OC = OA và góc quay $- \frac{{2\pi }}{3}$ nên phép quay ${Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}$ biến điểm C thành điểm A.

Vì OE = OC và góc quay $- \frac{{2\pi }}{3}$ nên phép quay ${Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}$ biến điểm E thành điểm C.

Vậy phép quay ${Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}$ biến tam giác ACE thành tam giác ECA hay biến tam giác ACE thành chính nó.