Trên miền đa giác không gạch chéo ở Hình 6, hãy: a) tìm GTLN của F = 2x + 3y; b) tìm GTNN của G = x – 4y
Bài 4 trang 36 SBT Toán 10 Tập 1: Trên miền đa giác không gạch chéo ở Hình 6, hãy:
a) tìm GTLN của F = 2x + 3y;
b) tìm GTNN của G = x – 4y.
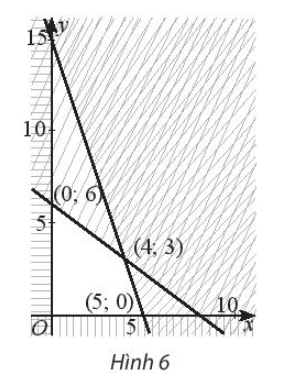
Miền đa giác không gạch chéo ở Hình 6 có tọa độ các đỉnh là (0; 0), (0; 6), (4; 3) và (5; 0).
a) Người ta chứng minh được rằng biểu thức F = 2x + 3y đạt GTLN tại các đỉnh của đa giác không bị gạch trên Hình 6.
Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0
F(0; 6) = 2 . 0 + 3 . 6 = 18
F(4; 3) = 2 . 4 + 3 . 3 = 14
F(5; 0) = 2 . 5 + 3 . 0 = 10.
Vì 0 < 10 < 14 < 18 nên GTLN của F là 18 tại đỉnh có tọa độ (0; 6).
b) Người ta chứng minh được rằng biểu thức G = x – 4y đạt GTNN tại các đỉnh của đa giác không bị gạch trên Hình 6.
Ta có: G(0; 0) = 0 – 4 . 0 = 0
G(0; 6) = 0 – 4 . 6 = – 24
G(4; 3) = 4 – 4 . 3 = – 8
G(5; 0) = 5 – 4 . 0 = 5
Vì – 24 < – 8 < 0 < 5 nên GTNN của G là – 24 tại đỉnh có tọa độ (0; 6).
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Bất phương trình bậc nhất hai ẩn