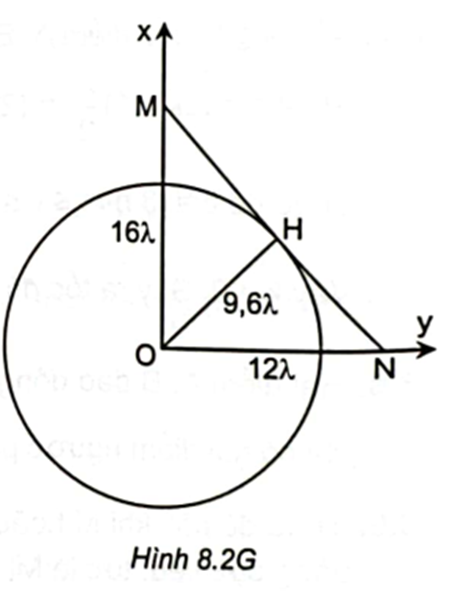
Trên mặt thoáng của một chất lỏng, một mũi nhọn $O$ chạm vào mặt thoáng dao động điều hoà với tần số $f$, tạo thành sóng trên mặt thoáng với bước sóng $\lambda$. Xét hai phương truyền sóng $Ox$ và $Oy$ vuông góc với nhau. Gọi ${\rm{M}}$ là một điểm thuộc Ox cách O một đoạn $16\,\lambda$và N thuộc Oy cách O một đoạn $12\,\lambda$. Tính số điểm dao động đồng pha với nguồn ${\rm{O}}$ trên đoạn ${\rm{MN}}$ (không kể ${\rm{M}},{\rm{N}}$).

Vị trí của các điểm O, M, N được mô tả như trên Hình 8.2G. Kẻ $OH \bot MN,{\rm{\Delta }}OMN$ vuông nên ta có: $\frac{1}{{{\rm{O}}{{\rm{H}}^2}}} = \frac{1}{{{\rm{O}}{{\rm{M}}^2}}} + \frac{1}{{{\rm{O}}{{\rm{N}}^2}}} \Rightarrow {\rm{OH}} = 9,6\lambda$

Các điểm dao động cùng pha với O, cách O những khoảng: $d = k\lambda$.

Xét trên đoạn MH có: $9,6\lambda \le {\rm{k}}\lambda \le 16\lambda \Rightarrow 9,6 \le {\rm{k}} \le 16$

$\Rightarrow {\rm{k}} = 10,11, \ldots 16$, vậy trên MH có 7 điểm.

Xét trên đoạn NH có: $9,6\lambda \le k\lambda \le 12\lambda \Rightarrow 9,6 \le k \le 12$

$\Rightarrow {\rm{k}} = 10,11,12$, vậy trên MH có 3 điểm.

Như vậy, tổng số điểm dao động cùng pha với ${\rm{O}}$ trên ${\rm{MN}}$ là 10 điểm.