Trên đường tròn lượng giác hãy biểu diễn các góc lượng giác có số đo có dạng là:

b) $k\frac{\pi }{4}\left(k\in \mathbb{Z}\right)$.

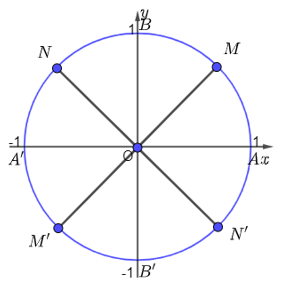
b) Với k = 0 thì có góc lượng giác có số đo góc là 0, được biểu diễn bởi điểm A;

Với k = 1 thì có góc lượng giác có số đo góc là $\frac{\pi }{4}$, được biểu diễn bởi điểm M;

Với k = 2 thì có góc lượng giác có số đo góc là $\frac{2\pi }{4}=\frac{\pi }{2}$ được biểu diễn bởi điểm B;

Với k = 3 thì có góc lượng giác có số đo góc là $\frac{3\pi }{4}$ được biểu diễn bởi điểm N;

Với k = 4 thì có góc lượng giác có số đo góc là $\frac{4\pi }{4}=\pi$ được biểu diễn bởi điểm A’;

Với k = 5 thì có góc lượng giác có số đo góc là $\frac{5\pi }{4}$ được biểu diễn bởi điểm M’;

Với k = 6 thì có góc lượng giác có số đo góc là $\frac{6\pi }{4}=\frac{3\pi }{2}$ được biểu diễn bởi điểm B’;

Với k = 7 thì có góc lượng giác có số đo góc là $\frac{7\pi }{4}$ được biểu diễn bởi điểm N’;

Với k = 8 thì có góc lượng giác có số đo góc là $\frac{8\pi }{4}=2\pi +0$ nên được biểu diễn bởi điểm A;

Vậy các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi các điểm A, M, B, N, A’, M’, B’, N’.  Khi đó ta có hình vẽ sau: