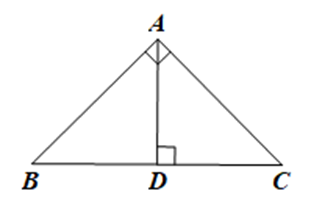
Tính độ dài đường cao AD làm tròn kết quả đến hàng phần trăm của centimét
Cho tam giác ABC vuông cân tại A có độ dài cạnh góc vuông AB và AC là 4 cm. Kẻ đường cao AD của tam giác ABC.
Tính độ dài đường cao AD (làm tròn kết quả đến hàng phần trăm của centimét).