Cho tam giác ABC vuông cân tại A. Qua A kẻ đường thẳng d bất kì sao cho đường thẳng d không cắt đoạn thẳng BC. Gọi D, E lần lượt là hình chiếu của B, C trên đường thẳng d. Chứng minh AD2 + AE2 không phụ thuộc vào vị trí của đường thẳng d.
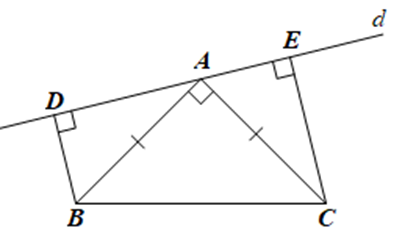
Do BD ⊥ d nên \(\widehat {ADB} = 90^\circ \), do đó tam giác ABD vuông tại D
Suy ra \(\widehat {ABD} + \widehat {BAD} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°) (1)
Mà \[\widehat {BAD} + \widehat {BAC} + \widehat {CAE} = 180^\circ \]
Suy ra \[\widehat {BAD} + \widehat {CAE} = 180^\circ - \widehat {BAC} = 180^\circ - 90^\circ = 90^\circ \] (2)
Từ (1) và (2) ta có \(\widehat {ABD} = \widehat {CAE}\).
Xét ∆ABD vuông tại D và ∆CAE vuông tại E có:
AB = CA, \(\widehat {ABD} = \widehat {CAE}\)
Do đó ∆ABD = ∆CAE (cạnh huyền – góc nhọn)
Suy ra AD = CE (hai cạnh tương ứng)
Khi đó AD2 + AE2 = CE2 + AE2 = AC2 (do tam giác CAE vuông tại E)
Vậy AD2 + AE2 không phụ thuộc vào vị trí của đường thẳng d.