Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết căn bậc hai của 18,75
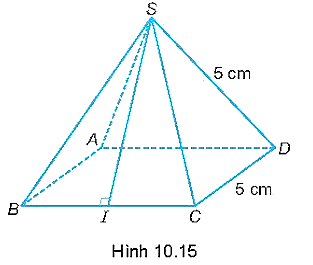
Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết \(\sqrt {18,75} \approx 4,3\).

Lời giải
Hình chóp tứ giác đều có mặt bên là các tam giác cân tại đỉnh và mặt đáy là hình vuông.
Suy ra SC = SD = 5 cm; BC = CD = 5 cm.
Tam giác SBC cân tại đỉnh S có SI là đường cao, đồng thời là trung tuyến hay I là trung điểm của BC, do đó IB = IC = \(\frac{{BC}}{2} = \frac{5}{2} = 2,5\) (cm).
Áp dụng định lý Pythagore vào tam giác SIC vuông tại I ta có:
SI2 + IC2 = SC2
Suy ra SI2 = SC2 – IC2 = 52 – (2,5)2 = 18,75.
Do đó, SI = \(\sqrt {18,75} \approx 4,3\) cm.
Diện tích xung quanh của hình chóp là:
\({S_{xq}} = p \cdot d \approx \frac{1}{2} \cdot 4 \cdot 5 \cdot 4,3 = 43\) (cm2).