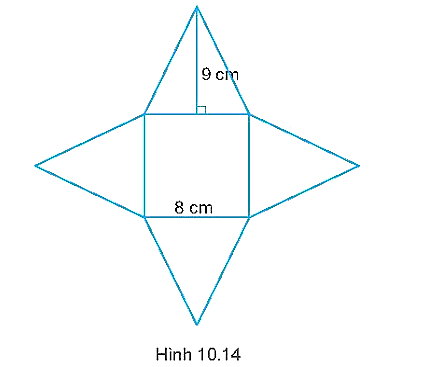
Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều. Tính diện tích toàn phần của tứ giác đều tạo thành.
6
29/10/2024
Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều. Tính diện tích toàn phần của tứ giác đều tạo thành.
Trả lời
Lời giải
Từ hình vẽ ta thấy hình chóp tứ giác đều được tạo thành cạnh đáy bằng 8 cm, trung đoạn bằng 9 cm.
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = p \cdot d = \frac{1}{2} \cdot 4 \cdot 8 \cdot 9 = 144\) (cm2).
Diện tích mặt đáy là: Sđ = 82 = 64 (cm2).
Diện tích toàn phần của hình chóp tứ giác đều là:
Stp = Sxq + Sđ = 144 + 64 = 208 (cm2).
