Tìm đường đi ngắn nhất từ đỉnh S đến T trong đồ thị trọng số ở Hình 17.
Tìm đường đi ngắn nhất từ đỉnh S đến T trong đồ thị trọng số ở Hình 17.
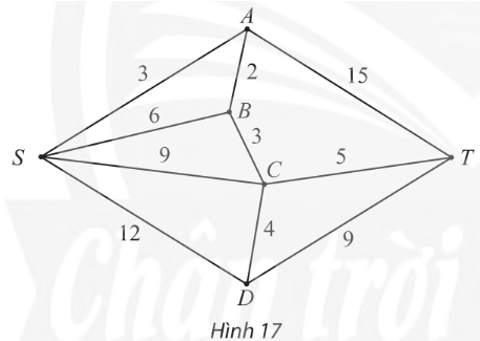
Tìm đường đi ngắn nhất từ đỉnh S đến T trong đồ thị trọng số ở Hình 17.

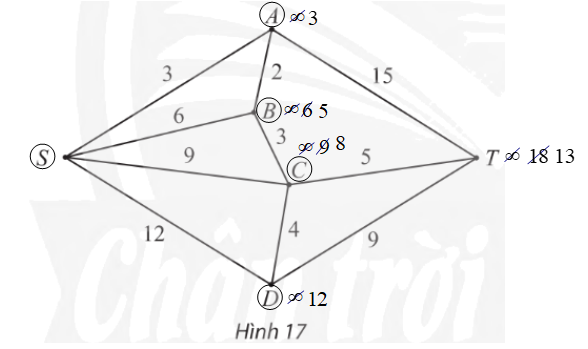
– Gán nhãn cho S bằng 0 (tức là, nS = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với S, gồm A, B, C, D. ta có:
⦁ nA = nS + wSA = 0 + 3 = 3. Vì 3 < ∞ nên ta đổi nhãn của A thành 3.
⦁ nB = nS + wSB = 0 + 6 = 6. Vì 6 < ∞ nên ta đổi nhãn của B thành 6.
⦁ nC = nS + wSC = 0 + 9 = 9. Vì 9 < ∞ nên ta đổi nhãn của C thành 9.
⦁ nD = nS + wSD = 0 + 12 = 12. Vì 12 < ∞ nên ta đổi nhãn của D thành 12.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là A nên ta khoanh tròn đỉnh A (đỉnh gần S nhất, chỉ tính các đỉnh khác S).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh A gồm B, T, ta có:
⦁ nB = nA + wAB = 3 + 2 = 5. Vì 5 < 6 (6 là nhãn hiện tại của B) nên ta đổi nhãn của B thành 5.
⦁ nT = nA + wAT = 3 + 15 = 18. Vì 18 < ∞ nên ta đổi nhãn của T thành 18.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần S thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B chỉ có đỉnh C, ta có:
nC = nB + wBC = 5 + 3 = 8. Vì 8 < 9 (9 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 8.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh C nên ta khoanh tròn đỉnh C (đỉnh gần S thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh C gồm D, T, ta có:
⦁ nD = nC + wCD = 8 + 4 = 12. Vì 12 cũng là nhãn hiện tại của D nên ta giữ nguyên nhãn của D là 12.
⦁ nT = nC + wCT = 8 + 5 = 13. Vì 13 < 18 (18 là nhãn hiện tại của T) nên ta đổi nhãn của T thành 13.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là đỉnh D nên ta khoanh tròn đỉnh D (đỉnh gần S thứ tư).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh D chỉ còn đỉnh T, ta có:
nT = nD + wDT = 12 + 9 = 21. Vì 21 > 13 (13 là nhãn hiện tại của T) nên ta giữ nguyên nhãn của T là 13.
Lúc này, ta thấy chỉ còn đỉnh T nên ta khoanh tròn đỉnh T (đỉnh gần S thứ năm).
– Nhìn lại các bước trên, ta thấy:
nT = 13 = nC + wCT
= nB + wBC + wCT
= nA + wAB + wBC + wCT
= nS + wSA + wAB + wBC + wCT
= wSA + wAB + wBC + wCT
= lSABCT.
Vậy SABCT là đường đi ngắn nhất từ S đến T, với độ dài bằng 13.