Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là A. AEC. B. AEFC. C. AC. D. AFC.
Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là
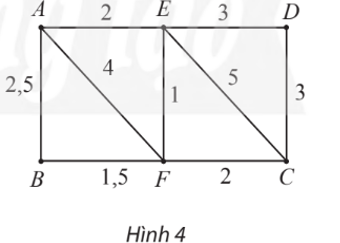
A. AEC.
B. AEFC.
C. AC.
D. AFC.
Cho đồ thị có trọng số như Hình 4. Đường đi ngắn nhất từ A đến C là

A. AEC.
B. AEFC.
C. AC.
D. AFC.
Đáp án đúng là: B
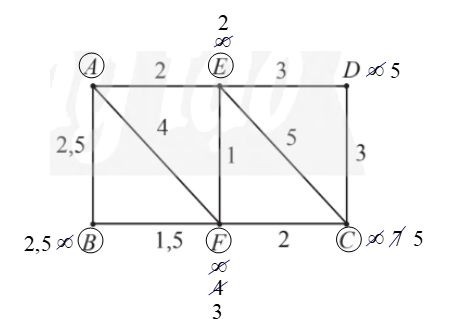
– Gán nhãn cho A bằng 0 (tức là, nA = 0), các đỉnh khác bằng ∞. Khoanh tròn đỉnh A.
– Tại các đỉnh kề với A, gồm E, F, B, ta có:
⦁ nE = nA + wAE = 0 + 2 = 2. Vì 2 < ∞ nên ta đổi nhãn của E thành 2.
⦁ nF = nA + wAF = 0 + 4 = 4. Vì 4 < ∞ nên ta đổi nhãn của F thành 4.
⦁ nB = nA + wAB = 0 + 2,5 = 2,5. Vì 2,5 < ∞ nên ta đổi nhãn của B thành 2,5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là E nên ta khoanh tròn đỉnh E (đỉnh gần A nhất, chỉ tính các đỉnh khác A).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh E gồm D, C, F, ta có:
⦁ nD = nE + wED = 2 + 3 = 5. Vì 5 < ∞ nên ta đổi nhãn của D thành 5.
⦁ nC = nE + wEC = 2 + 5 = 7. Vì 7 < ∞ nên ta đổi nhãn của C thành 7.
⦁ nF = nE + wEF = 2 + 1 = 3. Vì 3 < 4 (4 là nhãn hiện tại của F) nên ta đổi nhãn của F thành 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là B nên ta khoanh tròn đỉnh B (đỉnh gần A thứ hai).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh B chỉ có F, ta có:
nF = nB + wBF = 2,5 + 1,5 = 4. Vì 4 > 3 (3 là nhãn hiện tại của F) nên ta giữ nguyên nhãn của F là 3.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là F nên ta khoanh tròn đỉnh F (đỉnh gần A thứ ba).
– Trong các đỉnh chưa được khoanh tròn, đỉnh kề với đỉnh F chỉ có C, ta có:
nC = nF + wFC = 3 + 2 = 5. Vì 5 < 7 (7 là nhãn hiện tại của C) nên ta đổi nhãn của C thành 5.
Trong các đỉnh chưa được khoanh tròn, đỉnh có nhãn bé nhất là C, D (đều có nhãn là 5), nhưng do ta cần tìm đường đi ngắn nhất từ A đến C nên ta ưu tiên khoanh tròn đỉnh C (đỉnh gần A thứ tư).
– Nhìn lại các bước trên, ta thấy:
nC = 5 = nF + wFC
= nE + wEF + wFC
= nA + wAE + wEF + wFC
= wAE + wEF + wFC
= lAEFC.
Vậy AEFC là đường đi ngắn nhất từ A đến C, với độ dài bằng 5.
Do đó ta chọn phương án B.