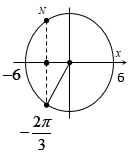
Một vật dao động điều hòa với phương trình x = 6cos(omegat - 2pi/3) cm
Một vật dao động điều hòa với phương trình x=6cos(ωt−2π3)cm, với ω>0. Kể từ t=0 đến t=16s, vật đi được quãng đường 9cm. Giá trị của ω là
A. 3πrad/s.
B. 2πrad/s.
C. 4πrad/s.
D. πrad/s.