Gọi x ³ 0, y ³ 0 lần lượt là số đơn vị vitamin A và B để một người cần dùng trong một ngày.
Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B nên ta có: 400 ≤ x + y ≤ 1000.
Hàng ngày, tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên ta có: x ≤ 600, y ≤ 500.
Mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A nên ta có: 0,5x ≤ y ≤ 3x.
Số tiền cần dùng mỗi ngày là: T (x, y) = 9x + 7,5.
Bài toán trở thành:
Tìm x ³ 0, y ³ 0 thỏa mãn hệ: \(\left\{ \begin{array}{l}0 \le x,\;y \le 600\\400 \le x + y \le 1000\\0,5x \le y \le 3x\end{array} \right.\) để T (x, y) = 9x + 7,5y đạt giá trị nhỏ nhất.
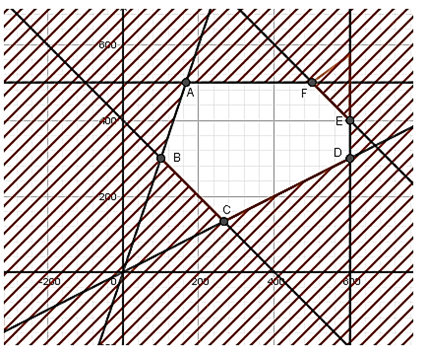
Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ như hình vẽ trên.
Miền nghiệm là lục giác ABCDEF với:
\(A\left( {\frac{{500}}{3};\;500} \right),\;B\left( {100;\;300} \right),\;C\left( {\frac{{800}}{3};\;\frac{{400}}{3}} \right),\;D\left( {600;\;300} \right),\;E\left( {600;\;400} \right),\;F\left( {500;\;500} \right)\)
Thay tọa độ các điểm A, B, C, D, E, F vào biểu thức T (x, y) = 9x + 7,5y và tìm GTNN của nó ta được:
\(T\;\left( {\frac{{500}}{3};\;500} \right) = 5250,\;T\;\left( {100;\;300} \right) = 3150,\;T\;\left( {\frac{{800}}{3};\;\frac{{400}}{3}} \right) = 3400\)
T (600; 300) = 7650, T (600; 400) = 8400, T (500; 500) = 8250
Suy ra min T (x; y) = 3150 khi x = 100; y = 300.
Vậy mỗi ngày, một người dùng 100 đơn vị Vitamin A, 300 đơn vị Vitamin B để chi phí rẻ nhất.